Регуляция уровня тестостерона в мужском организме
Совместные исследования с Уппсальским университетом (Швеция), Санкт-Петербургским
государственным университетом (Россия), Политехническим университетом Турина (Италия).
Тестостерон - основной андрогенный стероидный гормон. В регуляции уровня
тестостерона (Te) основную роль играют лютеинизирующий гормон
(LH - luteinizing hormone) и гонадотропин релизинг гормон
(GnRH - gonadotropin-releasing hormone). LH и GnRH гормоны генерируются в отделах
головного мозга, соответственно в гипофизе и гипоталамусе. Поэтому динамика LH и
особенно GnRH тесно связана с динамикой нейронов мозга и носит импульсный характер
[1 - 4]. При этом GnRH стимулирует секрецию LH. Как только LH достигает яичек
через кровь, он стимулирует специальные клетки в семенниках, называемые клетками
Лейдига. Эти клетки в конечном счете отвечают за выработку тестостерона у мужчин
(у женщин - специализированные клетки в яичниках, называемые клетками
тека (theca cells)). По мере повышения уровня тестостерона в сыворотке крови
в гипофиз и гипоталамус посылаются сигналы о прекращении стимуляции выработки
тестостерона. Таким образом Te подавляет секрецию GnRH и LH. С точки зрения
теории управления, клетки гипоталамуса, генерирующие GnRH, можно рассматривать
как импульсный элемент, осуществляющий амплитудно-частотную модуляцию. При этом
уровень Te выступает в качестве модулирующего сигнала, а уровень
GnRH - в качестве модулированного импульсного сигнала. С увеличением уровня Te
импульсы появляются реже, а их амплитуда уменьшается [1 - 4]. Что касается
наблюдаемого импульсного процесса секреции LH, то его можно рассматривать как
реакцию непрерывной части системы на импульсный сигнал,
поступающий от гипоталамуса [1 - 4].
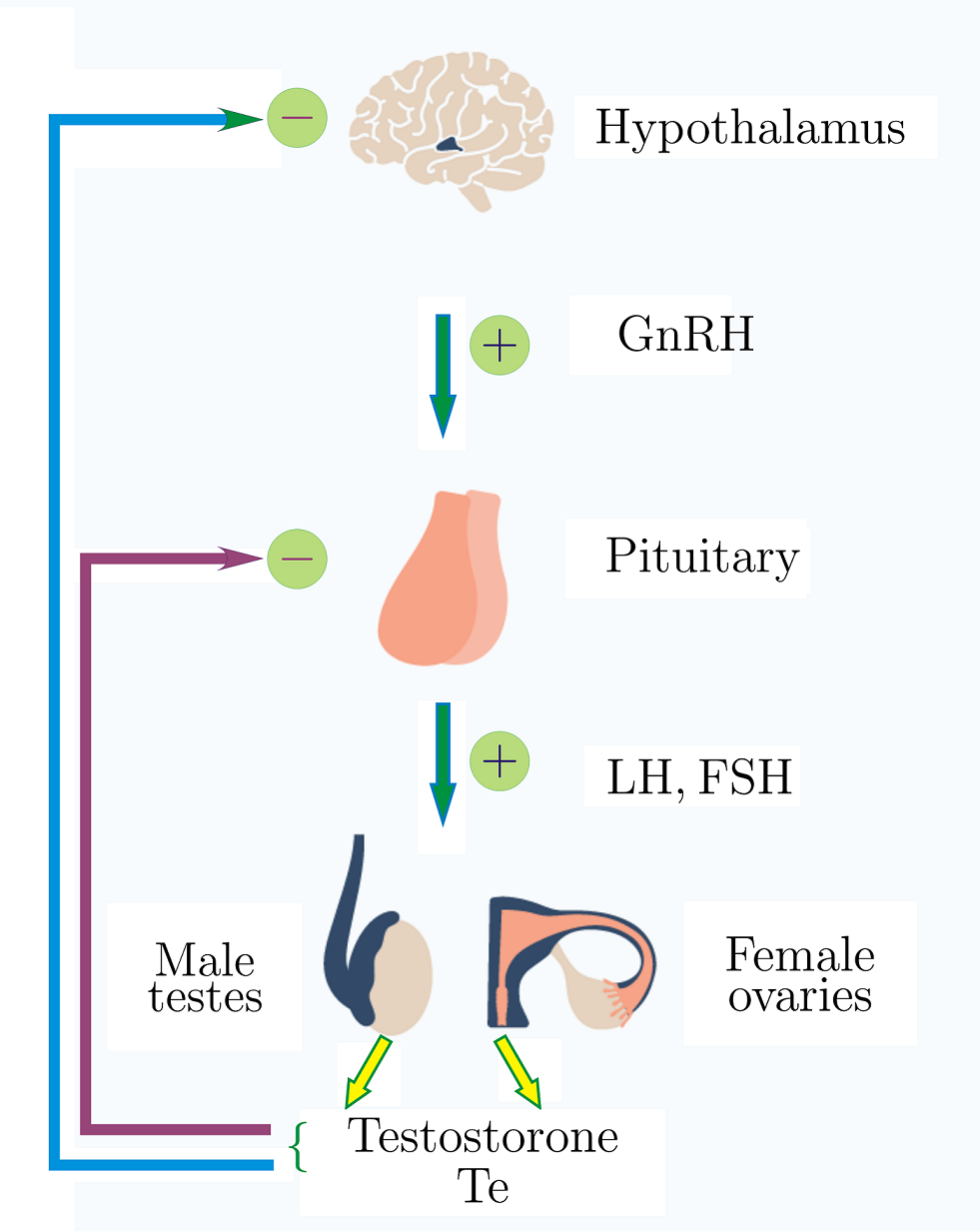
Схема гипоталамо-гипофизарно-тестикулярной оси. Здесь FSH - фолликулостимулирующий гормон (Follicle-Stimulating Hormone)
- А. В. Медведев, А. Н. Чурилов, А. И. Шепелявый, Стохастическая оптимизация в информатике, 2 (2006).
- A.N. Churilov, A. Medvedev, A.I. Shepeljavyi, Automatica, 45 (2009).
- A. N. Churilov and A. Medvedev, Automatica, 50 (2014).
- A.N. Churilov, A. Medvedev, P. Mattsson, IEEE Trans. Automatic Control, 59 (2014).
Импульсная модель регуляции уровня тестостерона у мужчин
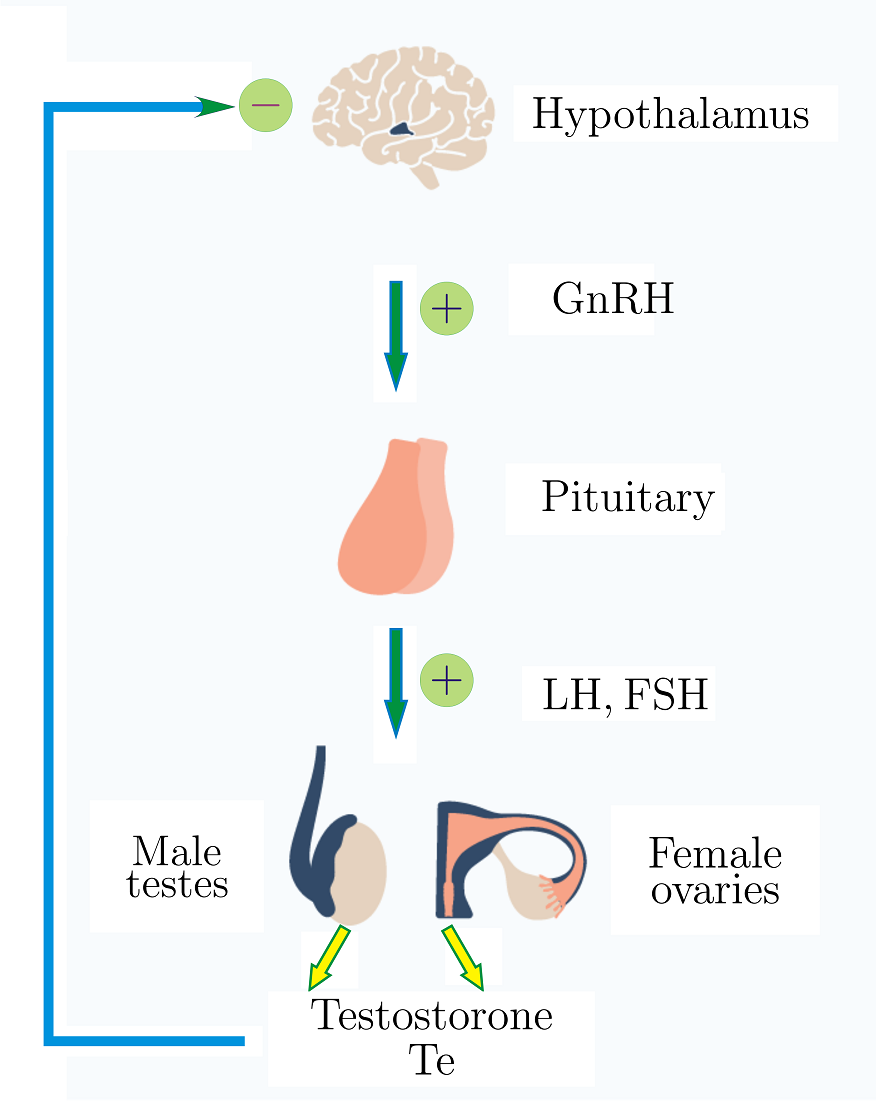
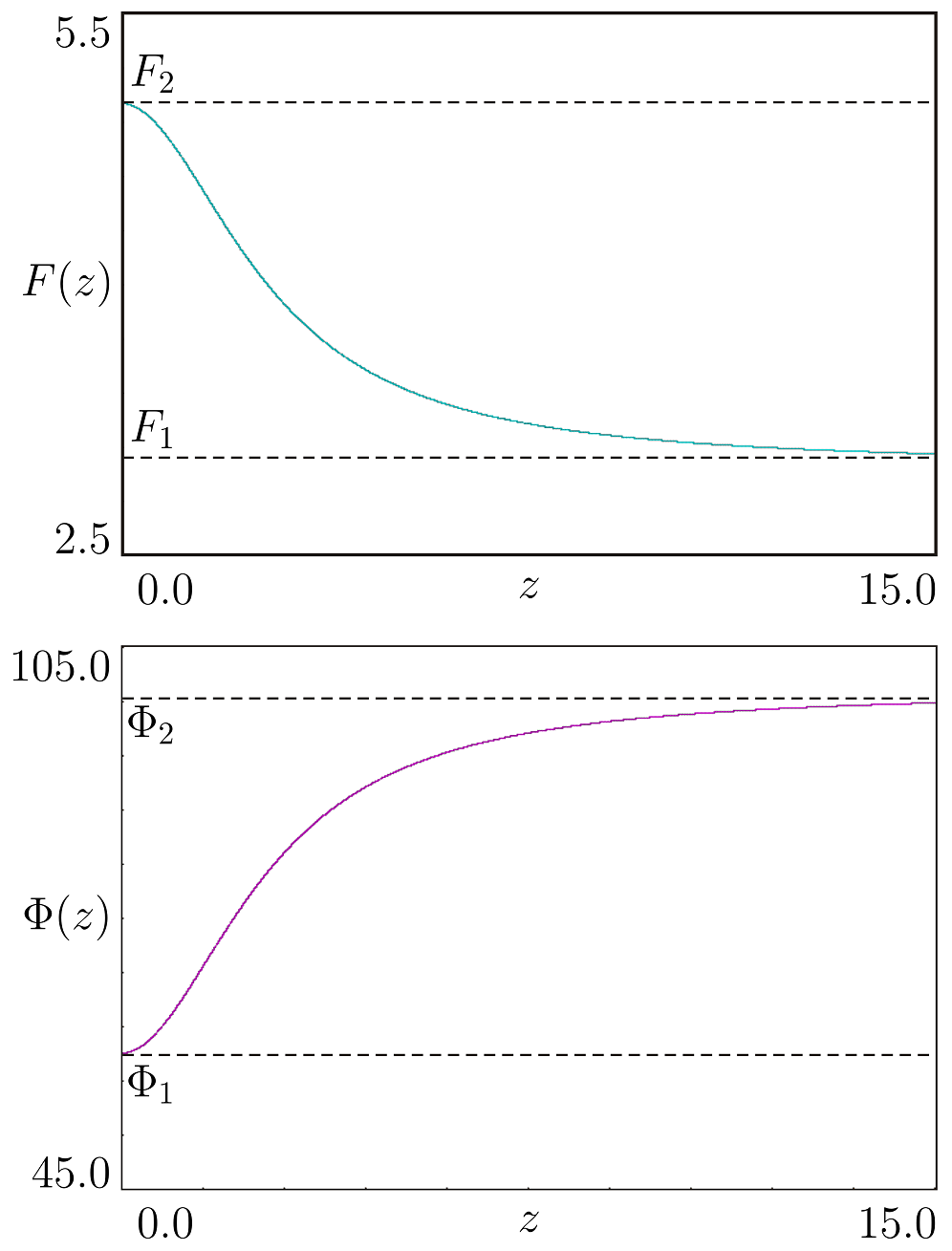
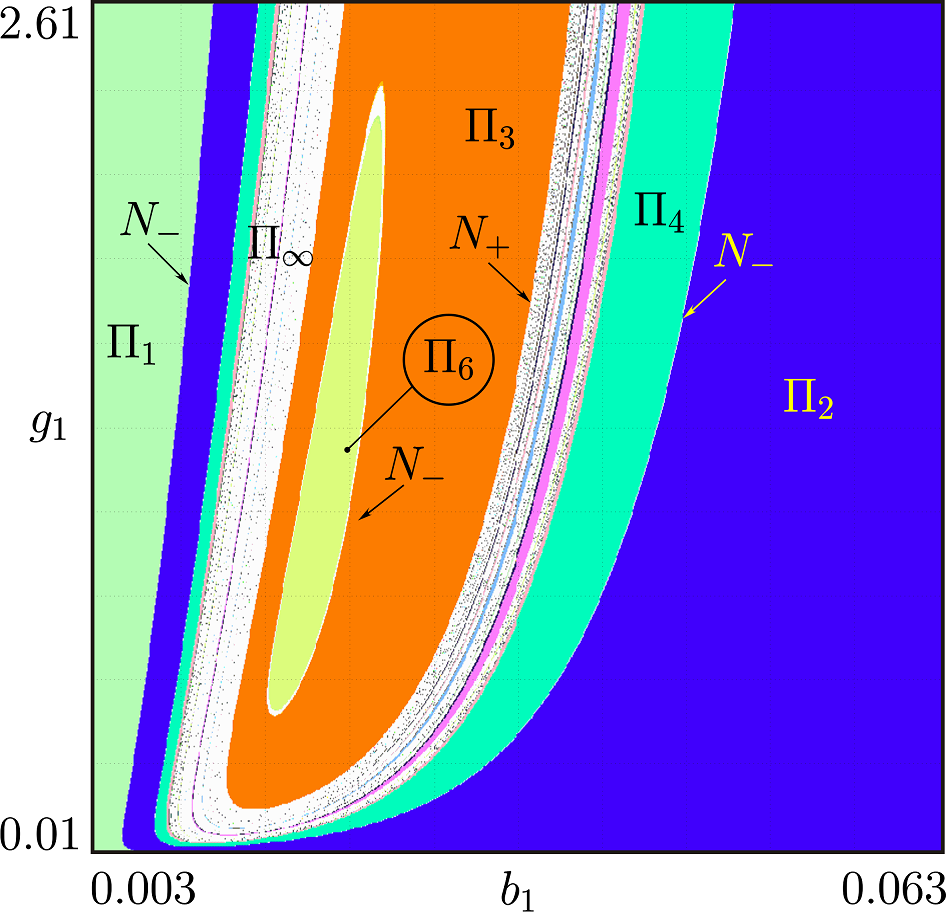
Математическая модель [A.N. Churilov, A. Medvedev, A.I. Shepeljavyi, Automatica, 45 (2009)]: \begin{gather*} \dot{x}=-b1\cdot x,\; \dot{y}=\mathrm{g}_1\cdot x-b_2\cdot y,\; \dot{z}=-b_3\cdot z+\mathrm{g}_2\cdot y,\; x(t_k^+)=x(t_k^-)+F (z(t_k)),\\ t_{k+1}=t_k+\Phi(z(t_k)),\; \Phi(z) = k_1 + k_2 \dfrac{(z/h)^p}{1 + (z/h)^p},\; F(z) = k_3 + \dfrac{k_4}{1 + (z/h)^p}. \end{gather*}
Здесь \(x=GnRH, y=LH, z=Te\) - концентрации гормонов; \( b_1,b_2,b_3,k_1,k_2,k_3,k_4,g_1 g_2,h\) и \(p\) - параметры.
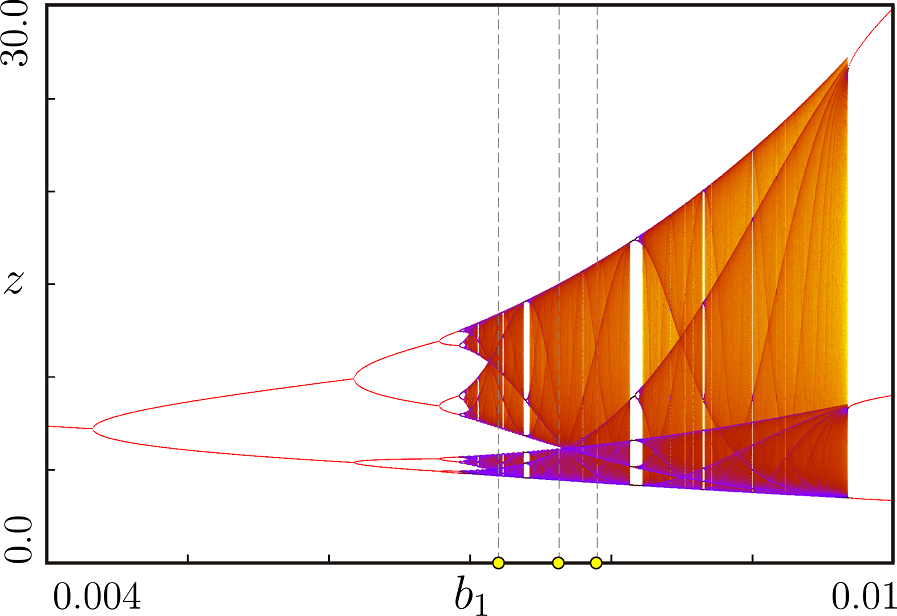
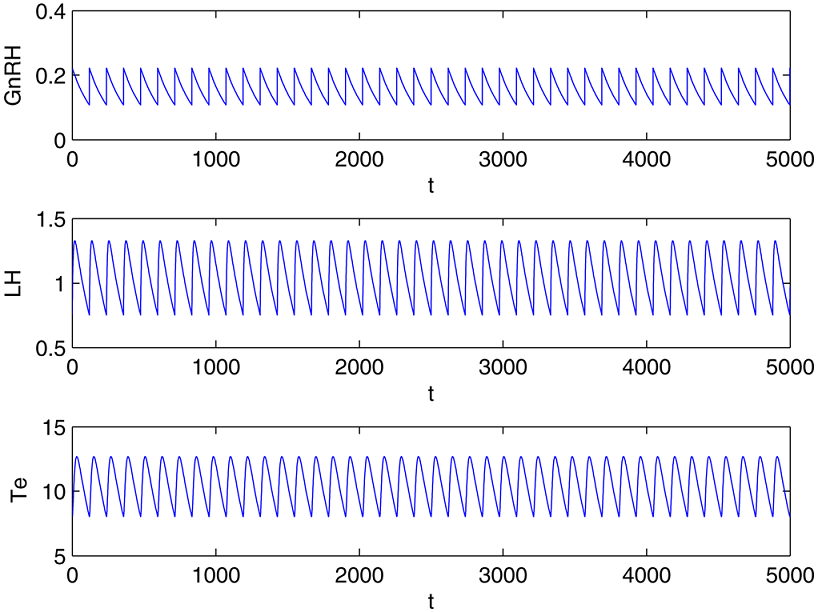
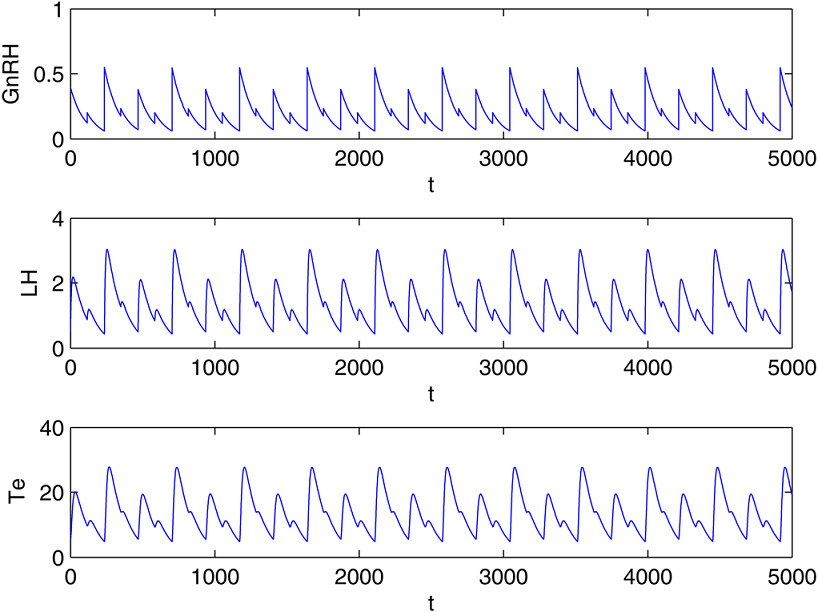
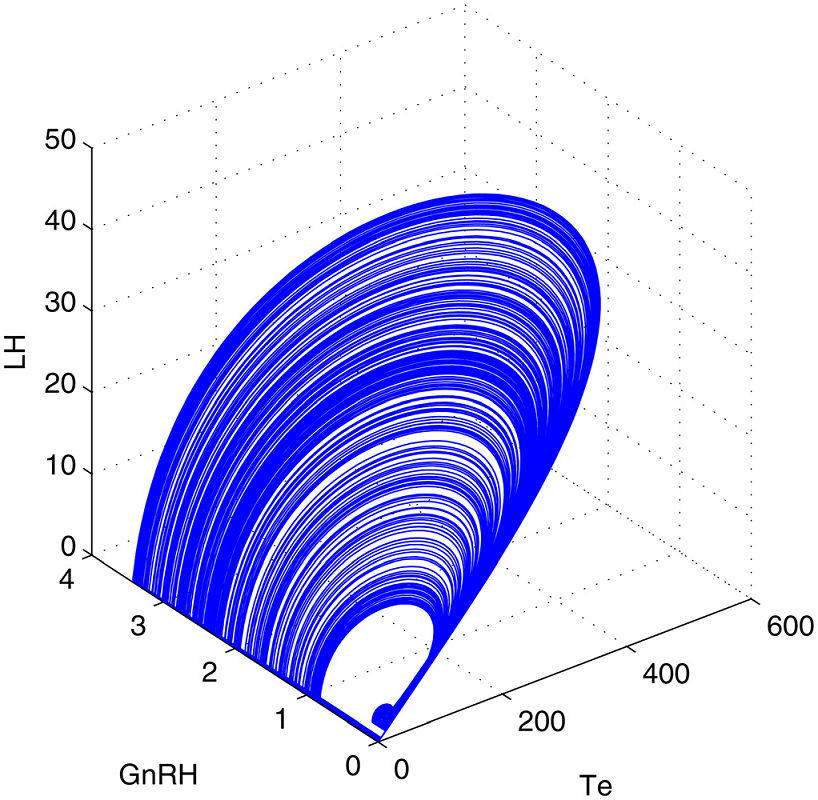
Переход к хаосу через классический каскад бифуркаций удвоения периода [1]
Импульсная модель регуляции уровня тестостерона с запаздыванием
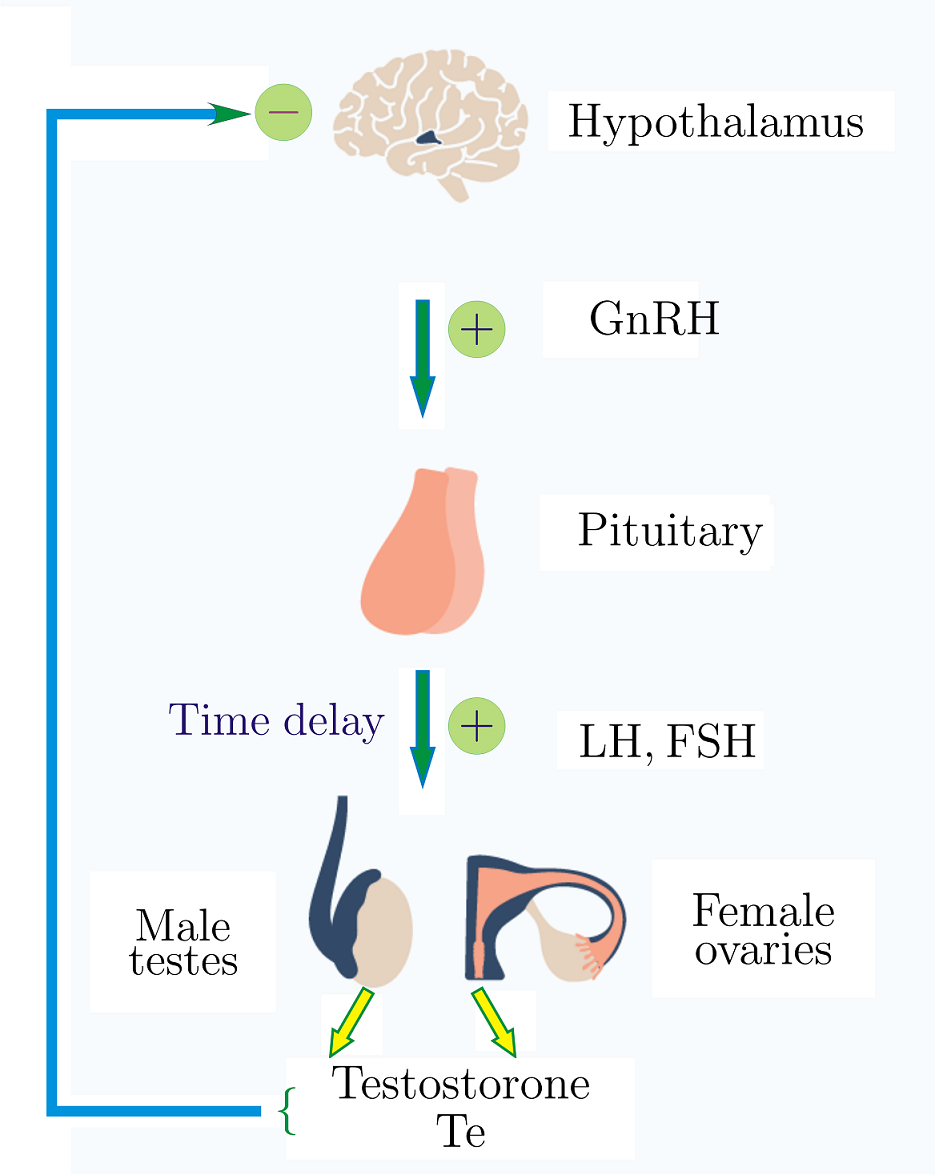Математическая модель (A. N. Churilov and A. Medvedev. Automatica, 50:2187-2190, 2014; A. N. Churilov, A. Medvedev, and P. Mattsson. IEEE Trans. Automatic Control, 59:728-733, 2014):
\begin{gather*} \dot{x}=-b1\cdot x,\;
\dot{y}=\mathrm{g}_1\cdot x-b_2\cdot y,\;\\
\dot{z}=-b_3\cdot z+\mathrm{g}_2\cdot y(t-\tau),\\
x(t_k^+)=x(t_k^-)+F (z(t_k)), t_{k+1}=t_k+\Phi(z(t_k)),\\
\Phi(z) = k_1 + k_2 \dfrac{(z/h)^p}{1
+ (z/h)^p},\; F(z) = k_3 + \dfrac{k_4}{1 + (z/h)^p}.
\end{gather*}
Параметры: \(b_1=0.048 \), \( b_1=0.055 \), \(b_2=0.15\), \(b_3=0.2\), \(g_1=2.0\), \( g_2=0.5\), \(p=2\), \(k_1=60.0\), \(k_2=\)
\(=40.0\), \(k_3=3.0\), \(k_4=2.0\), \(h=2.7\), \( 120<\tau<205.0 \), \( \forall\: n\geq 2 \quad T_n+T_{n-1}<\tau< T_n+T_{n-1}+T_{n-2} \) .
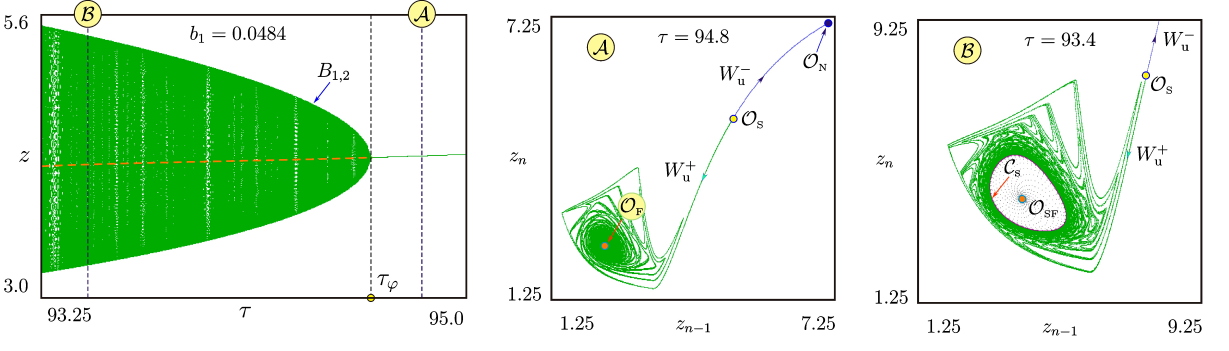
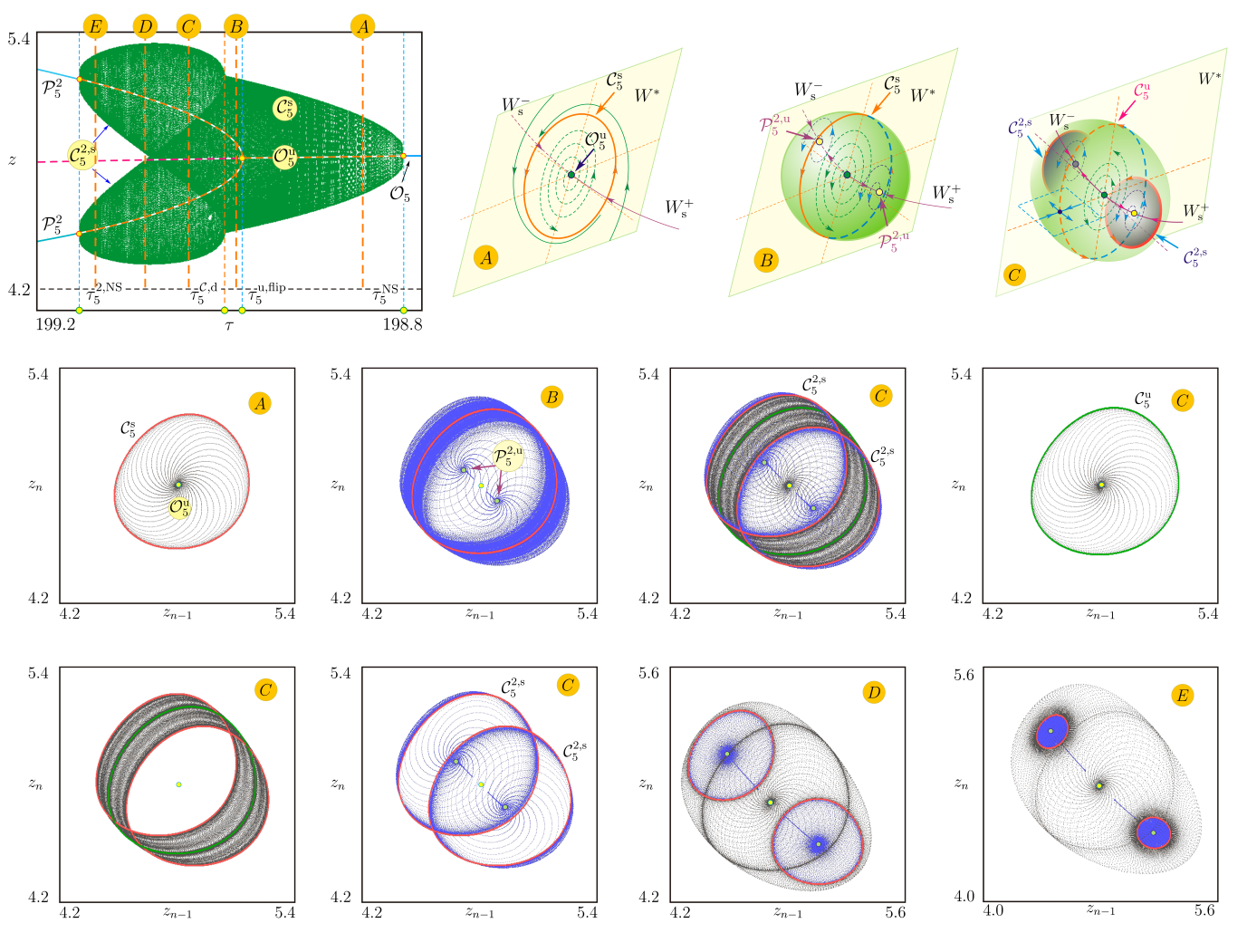
Параметры: \(b_1=0.048 \), \( b_1=0.055 \), \(b_2=0.15\), \(b_3=0.2\), \(g_1=2.0\), \( g_2=0.5\), \(p=2\), \(k_1=60.0\), \(k_2=\)
\(=40.0\), \(k_3=3.0\), \(k_4=2.0\), \(h=2.7\), \( 120<\tau<205.0 \), \( \forall\: n\geq 2 \quad T_n+T_{n-1}<\tau< T_n+T_{n-1}+T_{n-2} \) .
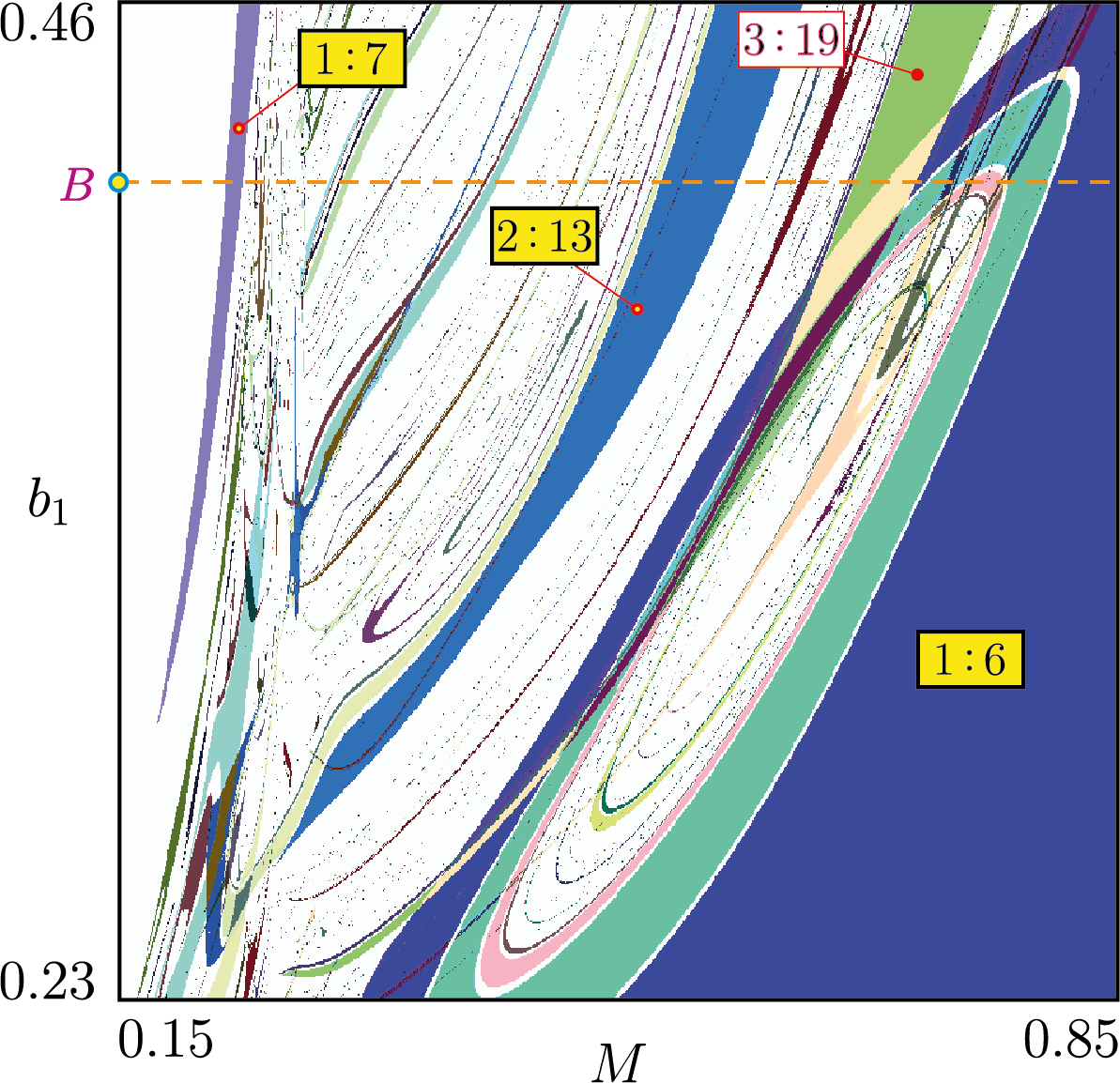
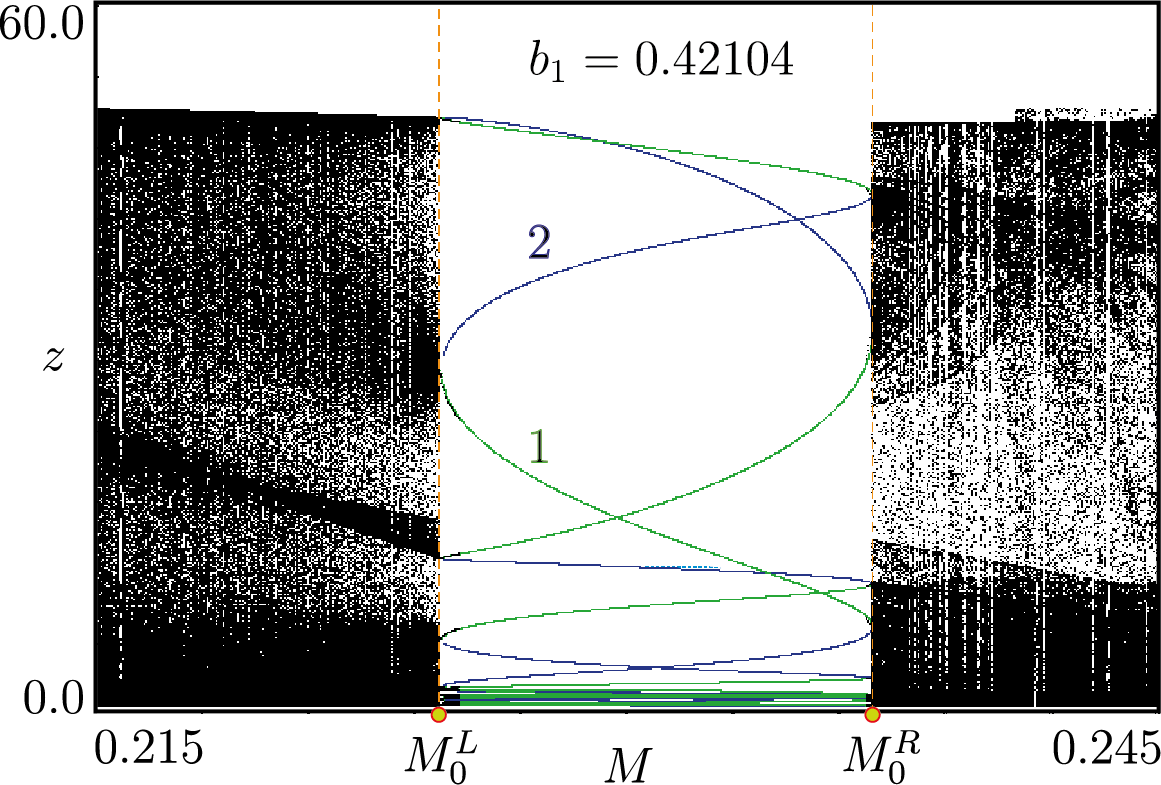
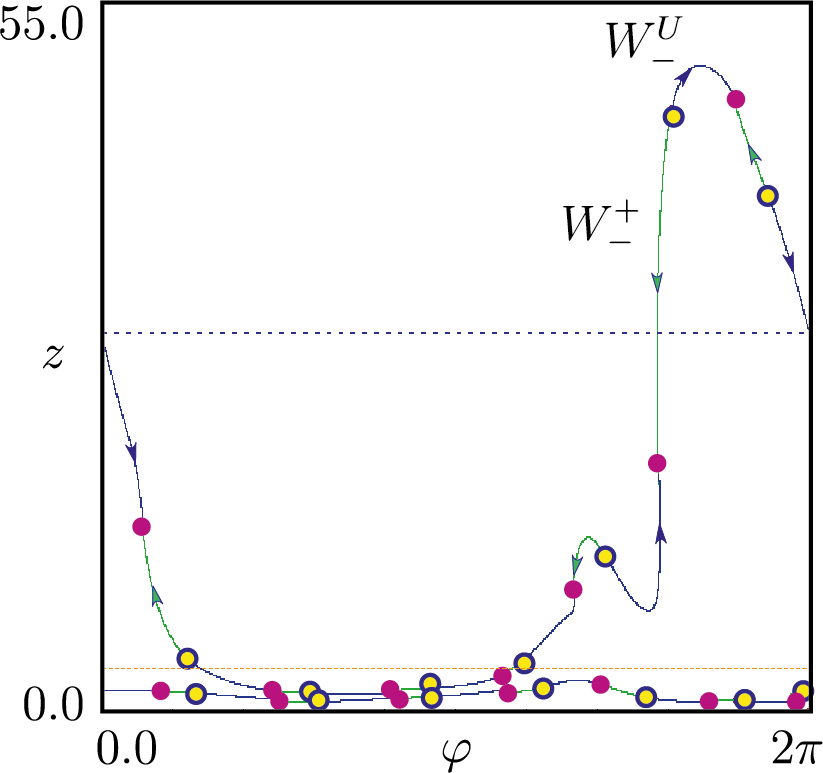
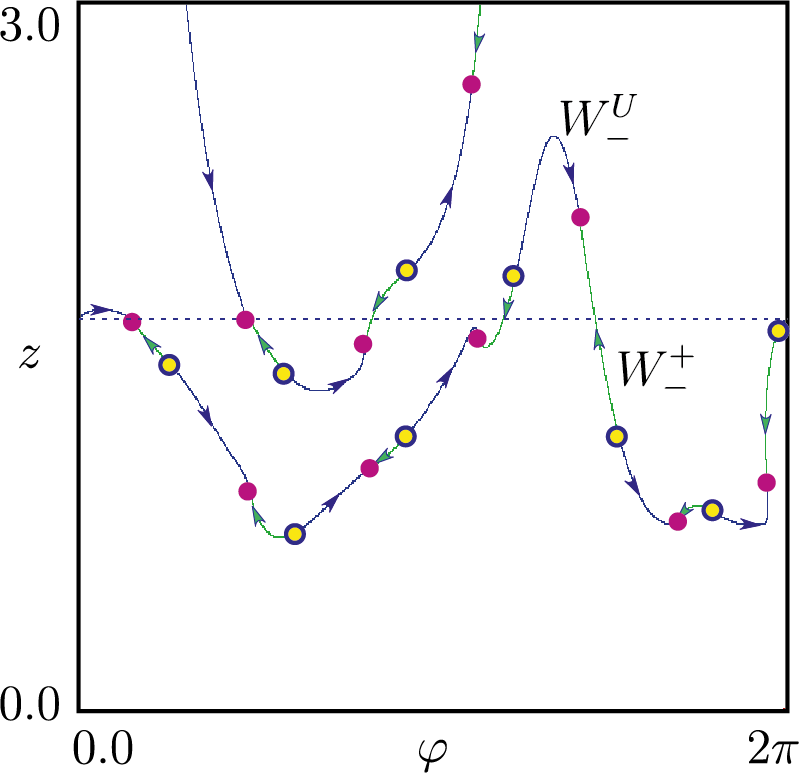
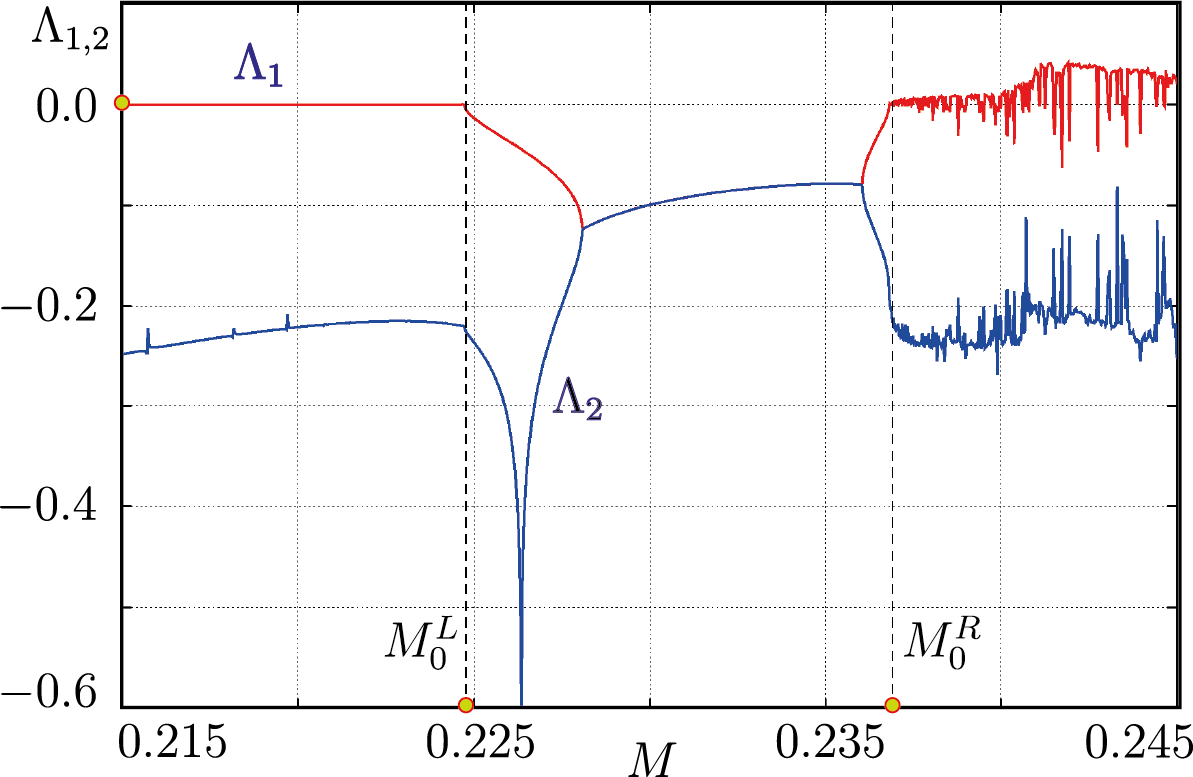
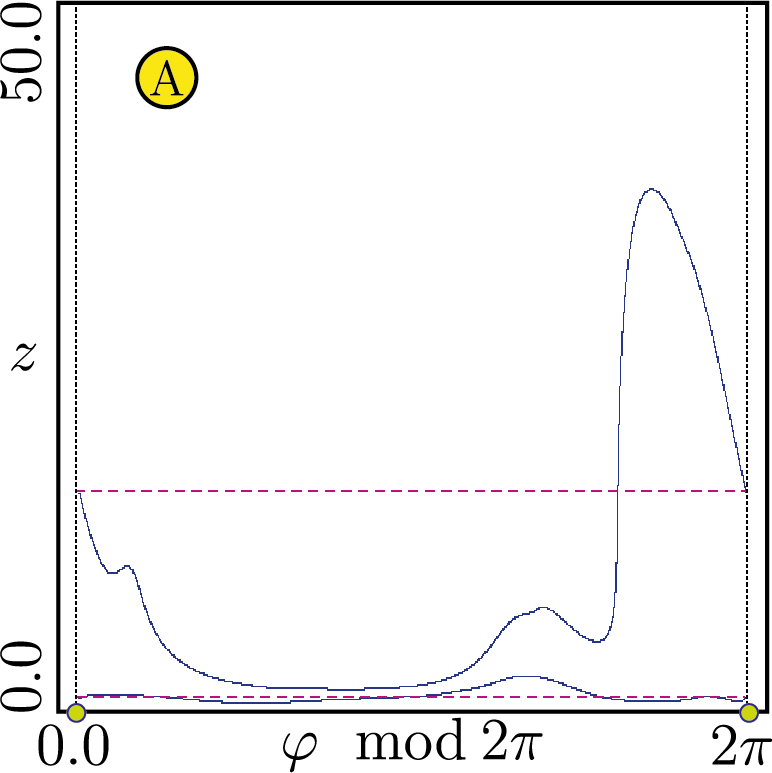
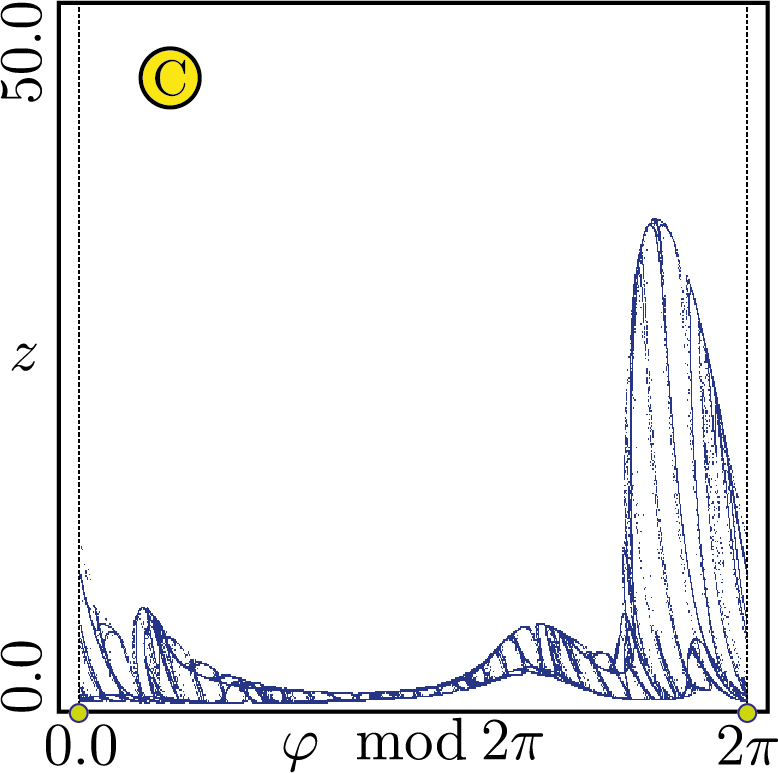
Влияние циркадного ритма на регуляцию уровня тестостерона
Математическая модель с дискретным временем \begin{align}\label{map_forced} x_{k+1}&=\text{e}^{-b_1 T_k}(x_k+\lambda_k),\\ y_{k+1}&=E_{21}(T_k)(x_k+\lambda_k)+\text{e}^{-b_2T_k}y_k,\notag\\ z_{k+1}&=E_{31}(T_k)(x_k+\lambda_k)+E_{32}(T_k)y_k+\text{e}^{-b_3T_k}z_k,\notag\\ \varphi_{k+1}&=\varphi_k+\omega \:T_k\:\: (\text{mod}\:\: 2\pi),\quad k=0,1,2,\dots,\notag \end{align} \begin{gather*} T_k=\Phi(\sigma_k),\quad\lambda_k=F(\sigma_k),\\ \sigma_k=z_k+\dfrac{M}{b_3^2+\omega^2}\left[b_3\sin (\varphi_k+\theta)-\omega\cos(\varphi_k+\theta)\right]+\dfrac{M}{b_3},\\ 0\leqslant \varphi_k\leqslant2\pi,\quad 0\leqslant \theta\leqslant2\pi. \end{gather*} Здесь \begin{gather*}\label{calc_zk} E_{21}(T)=\dfrac{g_1}{b_2-b_1}(\text{e}^{-b_1 T}-\text{e}^{-b_2 T} ), E_{32}(T)=\dfrac{g_2}{b_3-b_2}(\text{e}^{-b_2 T}-\text{e}^{-b_3 T} ), E_{31}(T)=\alpha_1\text{e}^{-b_1 T}+\alpha_2\text{e}^{-b_2 T}+\alpha_3\text{e}^{-b_3 T},\\ \alpha_1=\dfrac{g_1g_2}{(b_2-b_1)(b_3-b_1)}, \alpha_2=\dfrac{g_1g_2}{(b_1-b_2)(b_3-b_2)}, \alpha_3=\dfrac{g_1g_2}{(b_1-b_3)(b_2-b_3)}, \end{gather*} \begin{gather*} \Phi(\sigma)=k_1+k_2\dfrac{(\sigma/h)^p}{1+(\sigma/h)^p},\quad F(\sigma)=k_3+\dfrac{k_4}{1+(\sigma/h)^p}. \end{gather*}
