Отображения с большим числом границ (borders)

Однофазный инвертор с широтно-импульсным управлением
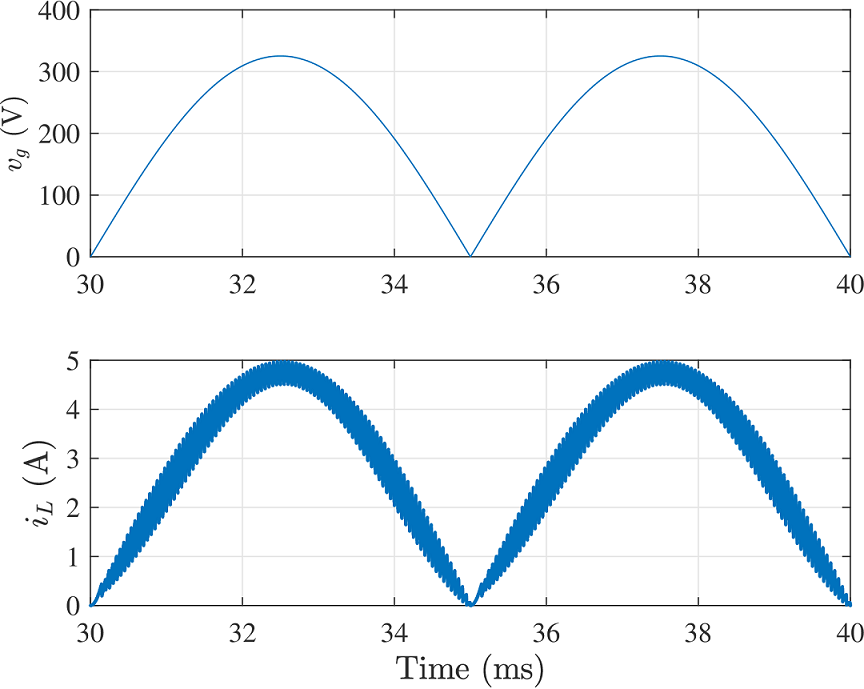
Регулярная динамика
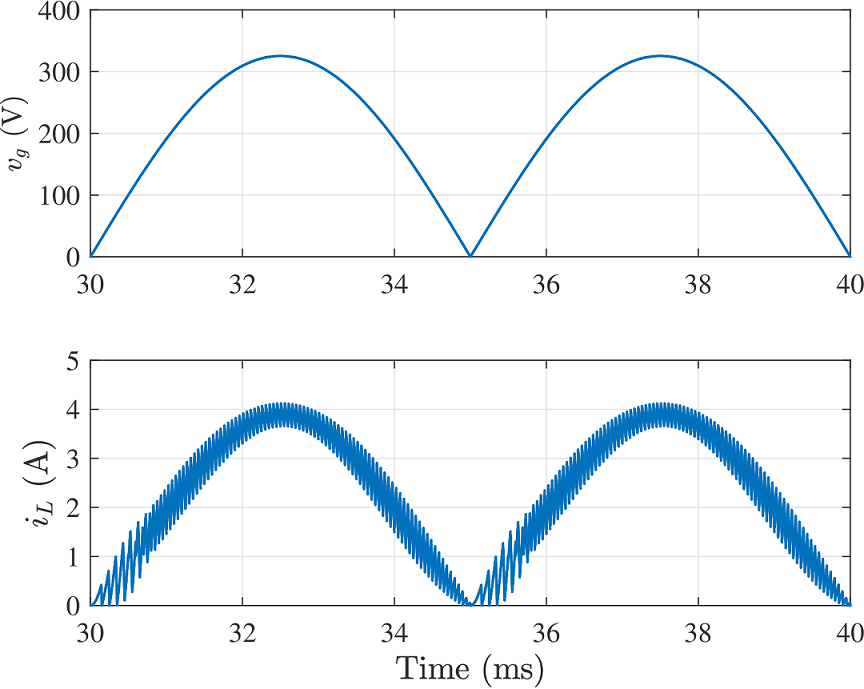
Хаотическая динамика
Математическая модель инвертора с непрерывным временем
$$
\frac{dx}{d\bar{t}}=
\begin{cases}
\lambda(x-1), &\:\:\:
x(\bar{t})\big|_{\bar{t}=\lfloor \bar{t} \rfloor} <
\dfrac{q}{\Gamma}\cos\left(\dfrac{2\pi \lfloor \bar{t} \rfloor}{m}\right)
-\dfrac{2P}{\alpha\Gamma}\left(\bar{t}-\lfloor \bar{t} \rfloor-\tfrac{1}{2}\right)
\\[.5em]
\lambda(x+1), &\:\:\:
x(\bar{t})\big|_{\bar{t}=\lfloor \bar{t} \rfloor} >
\dfrac{q}{\Gamma}\cos\left(\dfrac{2\pi \lfloor \bar{t} \rfloor}{m}\right)
-\dfrac{2P}{\alpha\Gamma}\left(\bar{t}-\lfloor \bar{t} \rfloor-\tfrac{1}{2}\right)
\end{cases}
$$
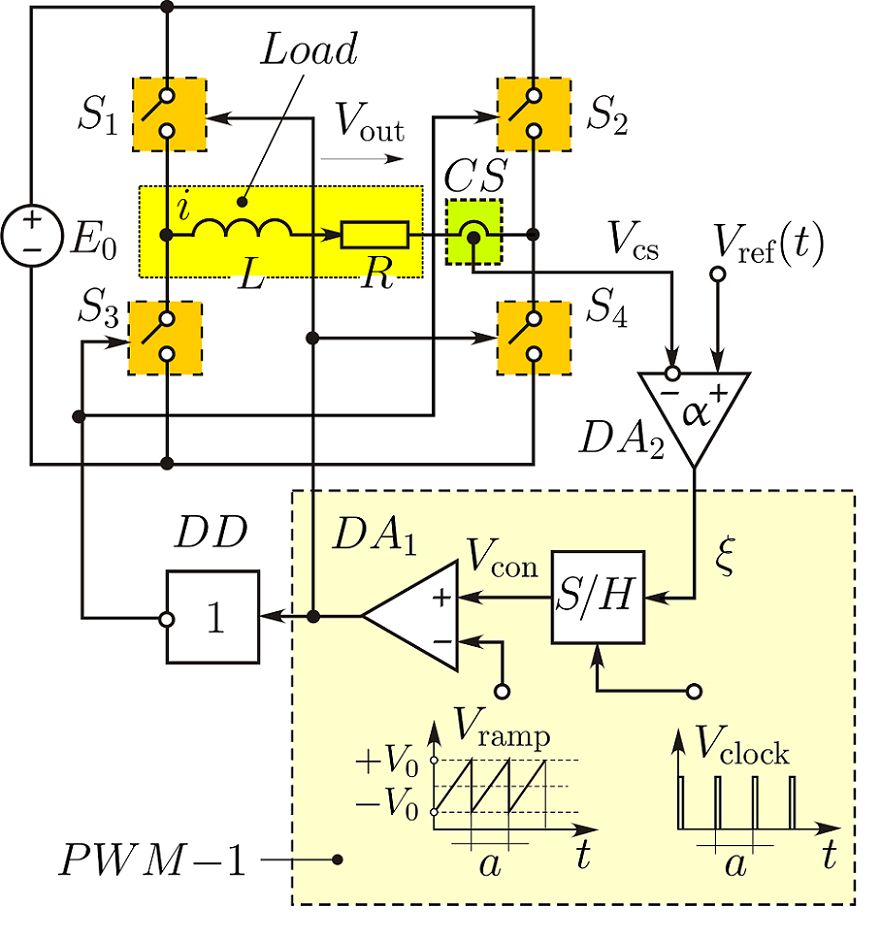
Схема инвертора
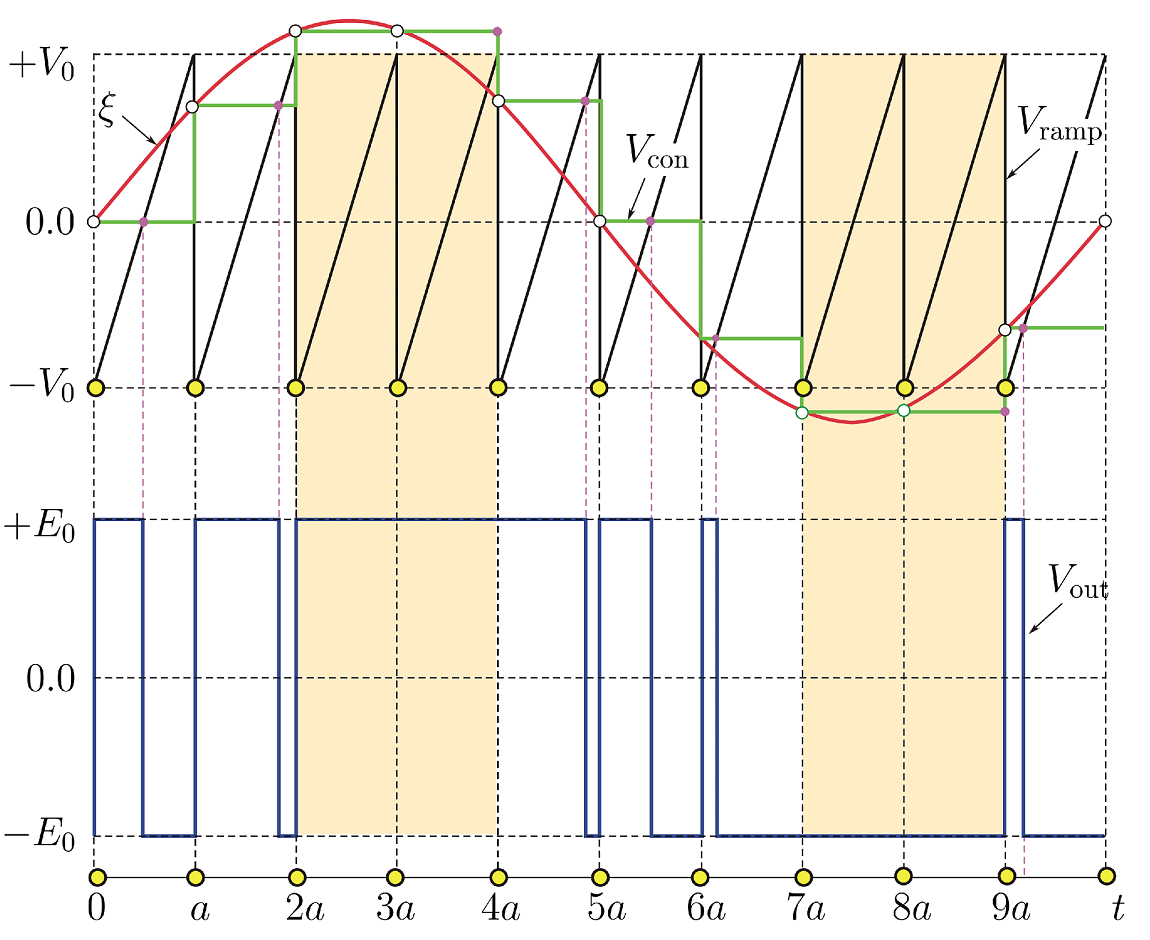
Временные диаграммы сигналов инвертора
\(
x=\dfrac{R i}{E_0},\
\overline{t}=\dfrac{t}{a},\
P=\dfrac{R}{\beta E_*}V_0,\
q=\dfrac{R}{\beta E_*}V_m,\
\lambda=-\dfrac{R}{L}a,\
\Gamma=\dfrac{E_0}{E_*},
\)
кратность частот \( m=\frac{f_{sw}}{f_{ref}}, \) 50 < m < 5000.
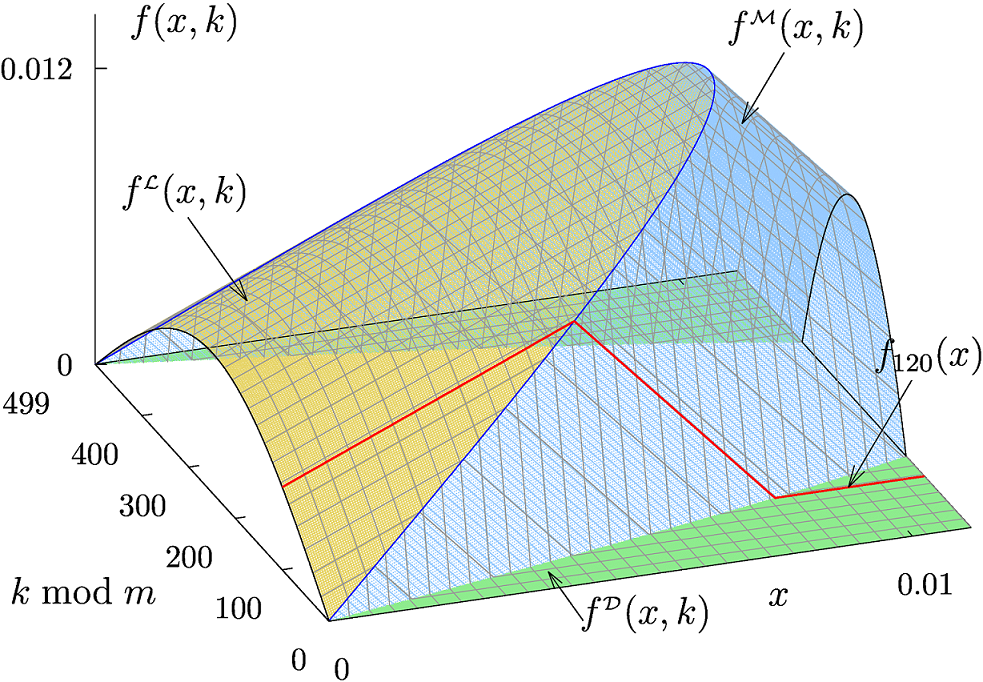
Математическая модель инвертора с дискретным временем
$$
F(x_k,k) =
\begin{cases}
F_L(x_k)=b x_k - (b-1),
&&\!\! &\!\!\!x_k\leq s^-_k,\\
F_M(x_k)=b x_k - (b+1)+2b^{(1-z_k)},
&&\!\! s^-_k < &\!\!\!x_k < s^+_k,\\
F_R(x_k)=b x_k + (b-1),
&&\!\! s^+_k\leq &\!\!\!x_k,
\end{cases}
$$
многообразие переключения:
$$
s^{\pm}_k=\dfrac{q}{\Gamma} \cos\left(\dfrac{2\pi k}{m}\right)
\pm\dfrac{P}{\alpha\Gamma},
$$
относительная длительность импульсов \( 0\leq z_k\leq 1.0 \):
$$
z_k =\dfrac{\alpha q}{2P}\cos\left(\dfrac{2\pi k}{m}\right)-
\dfrac{\alpha\Gamma}{2P}{x_k}+\dfrac{1}{2}.
$$
Насыщение модулятора:
$$
\begin{align}
x_k &\leq s^-_k \to& 1\\
s^-_k < x_k &< s^+_k \to& z_k\\
s^+_k&\leq x_k \to& 0.
\end{align}
$$
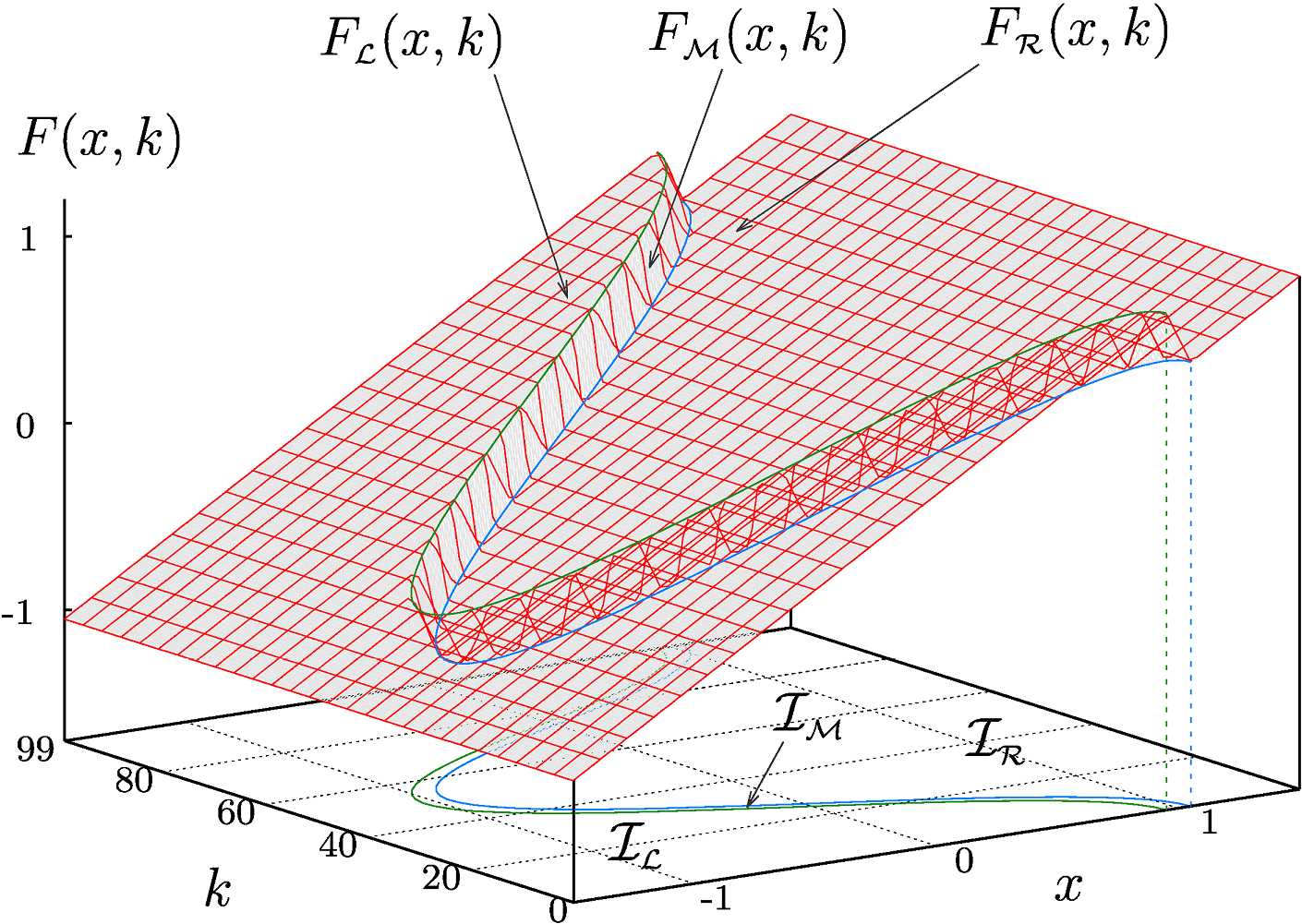
Двумерное отображение
Макроструктура пространства параметров
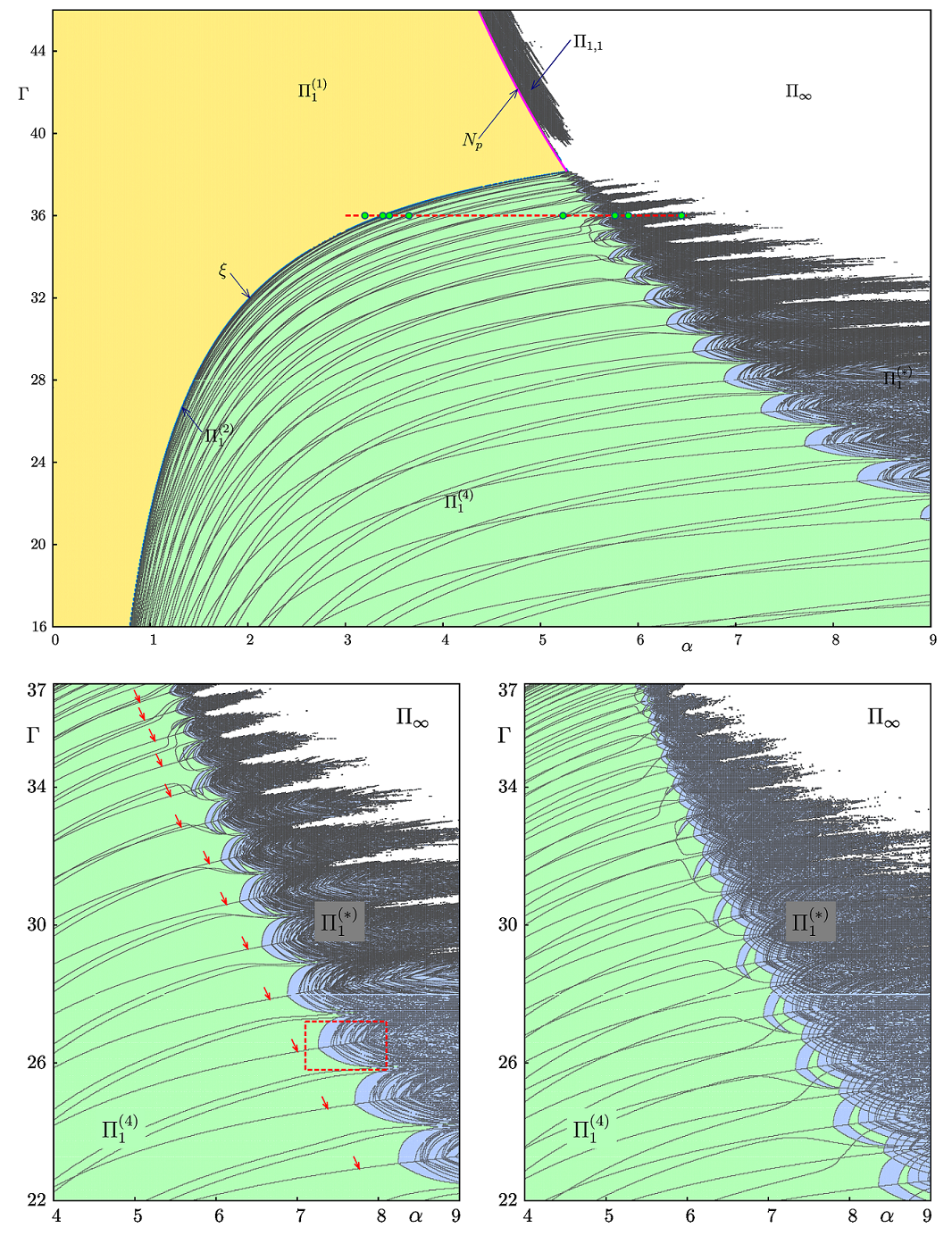

Различные типы периодических орбит в области \( \Pi_1 \)
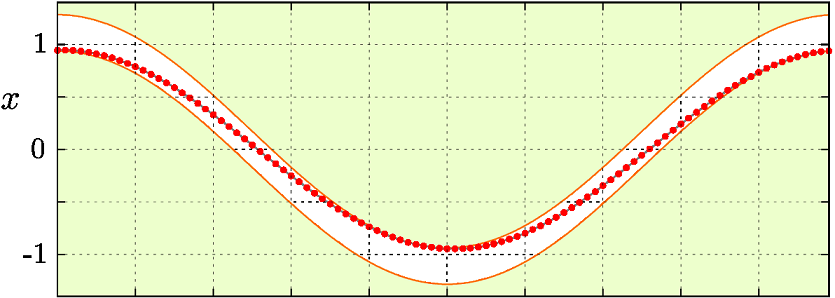
\( O_{M^m} \), область \(\Pi_1^{(1)} \subset \Pi_1 \)
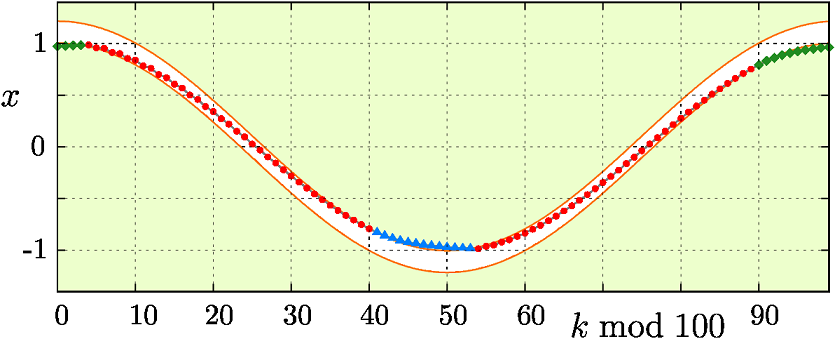
\( O_{M^{k_1}R^{k_2}M^{k_3}L^{k4}} \), где
\( k_1 + k_2 + k_3 + k_4 = m, \) область \(\Pi_1^{(4)}
\subset \Pi_1 \)
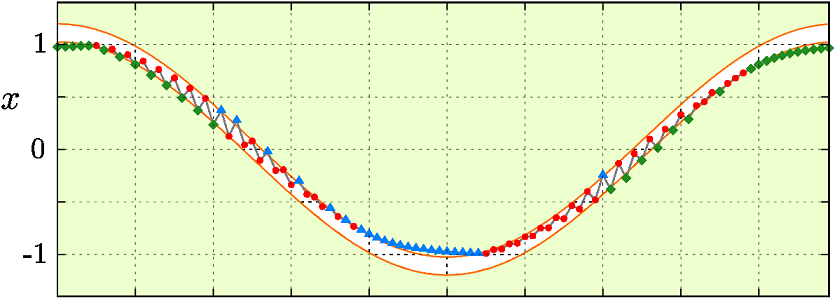
Более сложный тип периодических движений, область \(\Pi_1^{(*)}
\subset \Pi_1 \)
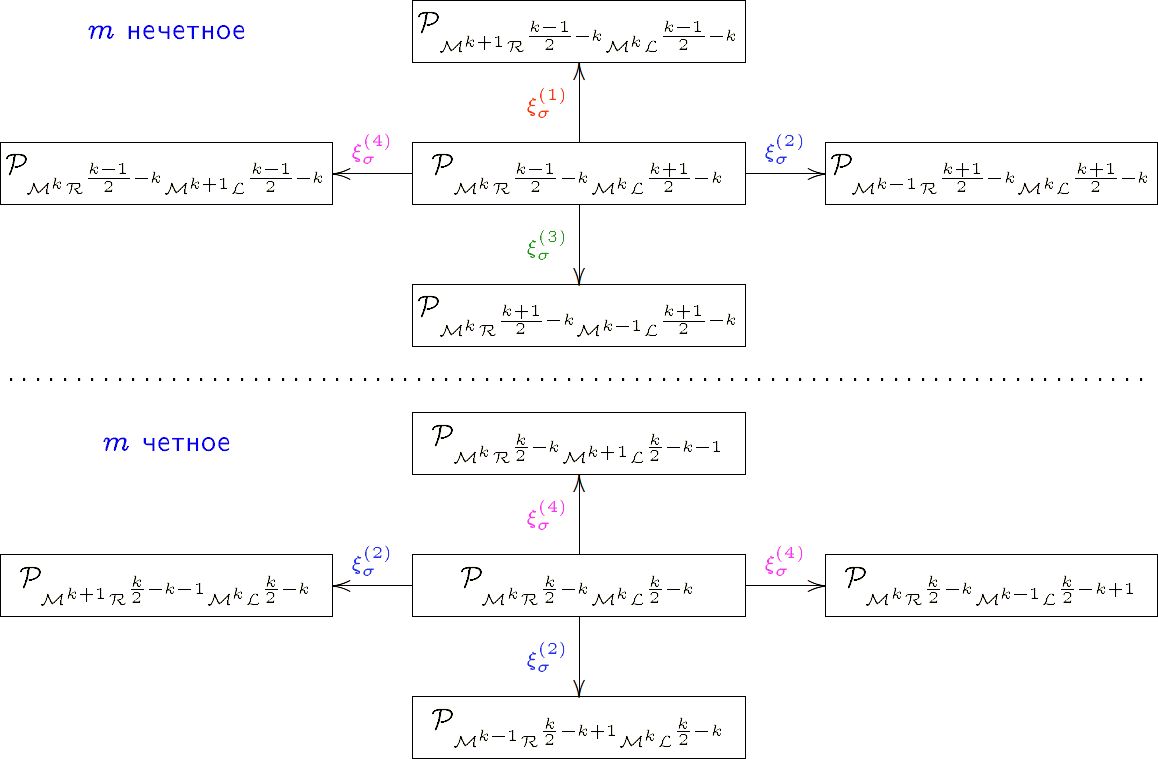
"Border collisions" в области \( \Pi_1 \)
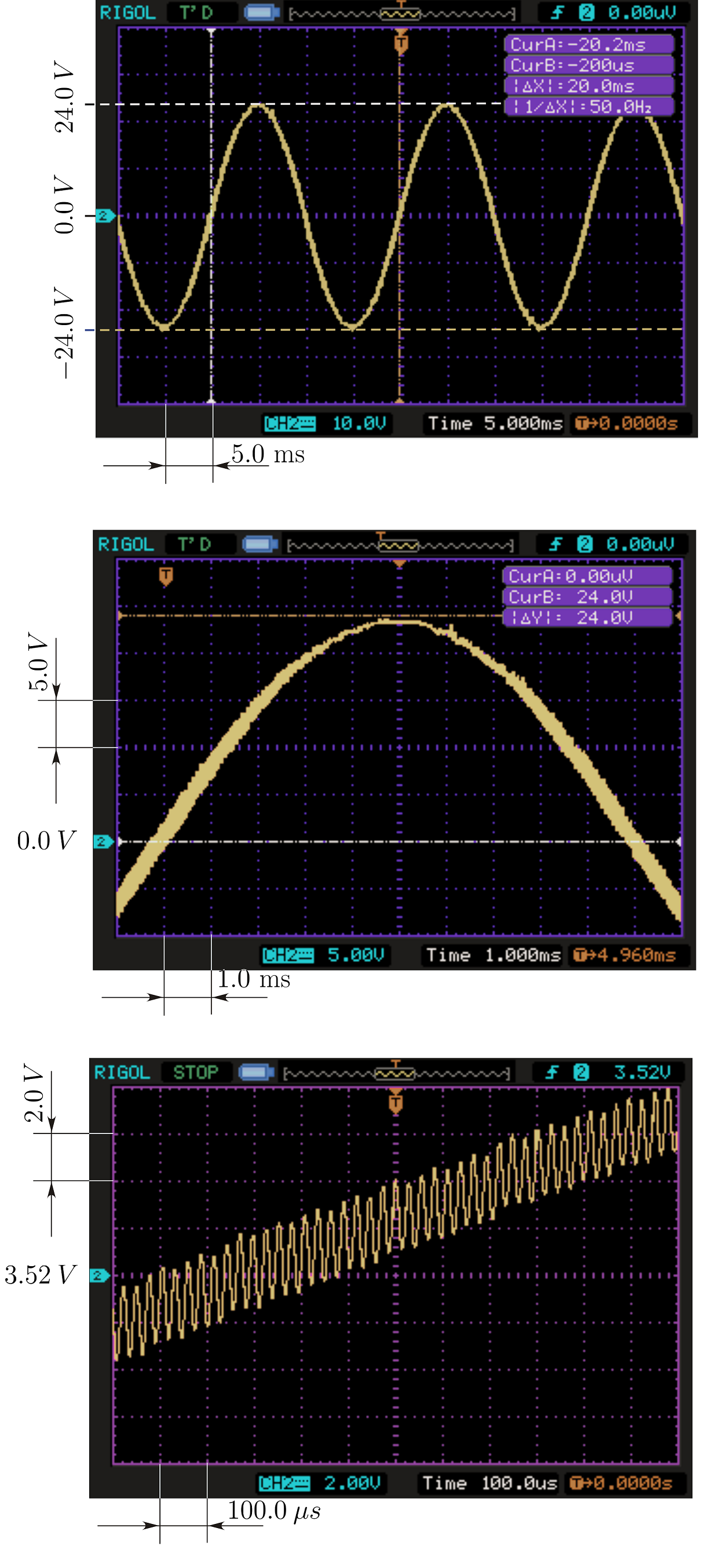
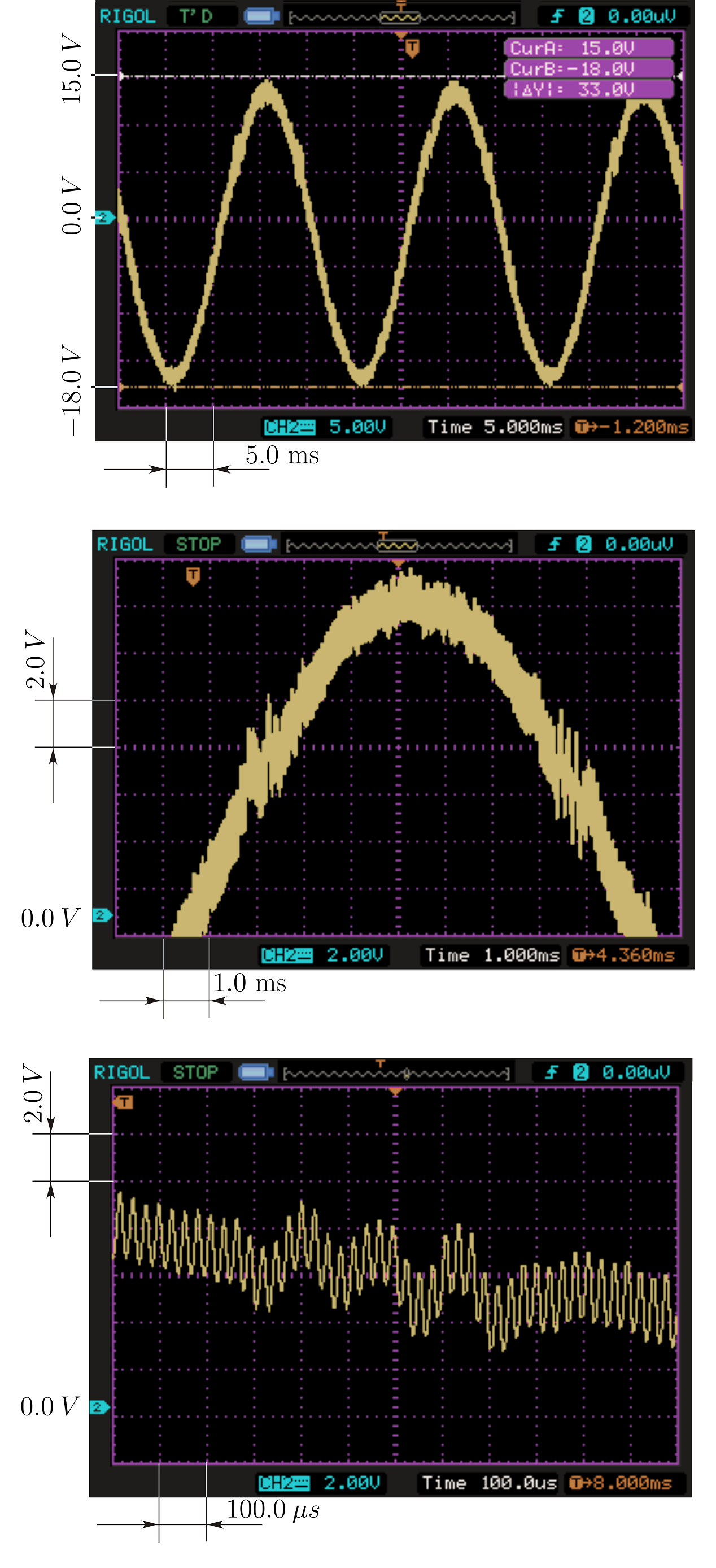
Исследование явления "bubbling"

Лаборатория проф. Abdelali El Aroudi, Department of Electronics, Electrical
Engineering and Automatic Control Universitat Rovira i Virgili, Tarragona,
Spain. Экспериментальное детектирование "bubbling" в однофазном инверторе.
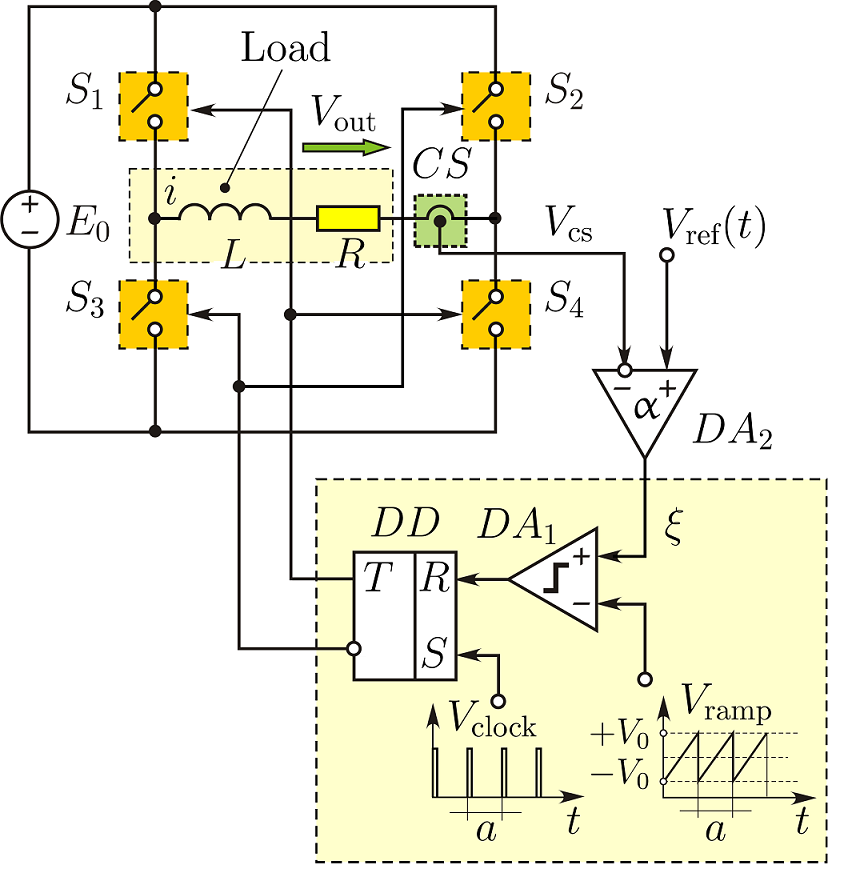
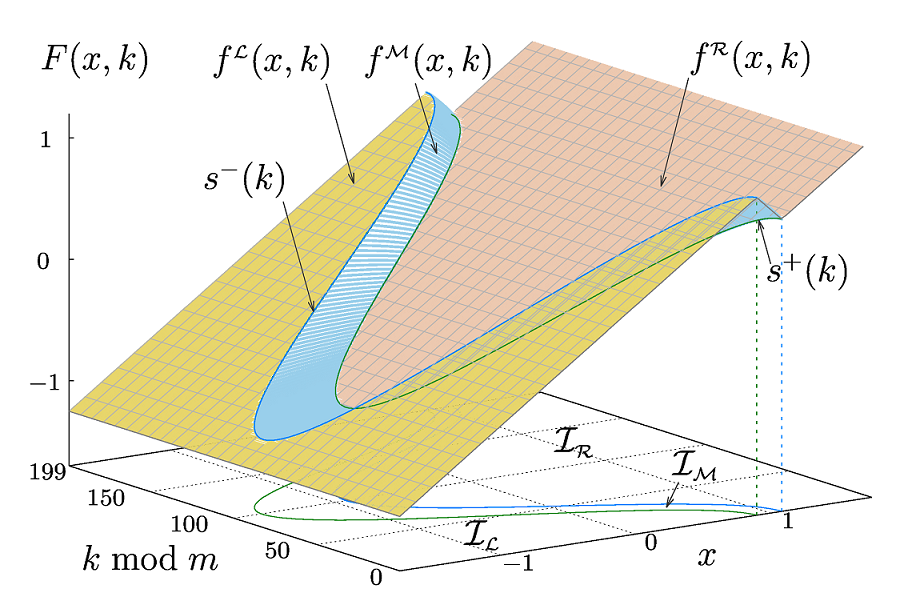

Схема инвертора

Временные диаграммы сигналов инвертора

Двумерное отображение
Макроструктура пространства параметров


Различные типы периодических орбит в области \( \Pi_1 \)

\( O_{M^m} \), область \(\Pi_1^{(1)} \subset \Pi_1 \)

\( O_{M^{k_1}R^{k_2}M^{k_3}L^{k4}} \), где
\( k_1 + k_2 + k_3 + k_4 = m, \) область \(\Pi_1^{(4)}
\subset \Pi_1 \)

Более сложный тип периодических движений, область \(\Pi_1^{(*)}
\subset \Pi_1 \)
"Border collisions" в области \( \Pi_1 \)

Исследование явления "bubbling"

Лаборатория проф. Abdelali El Aroudi, Department of Electronics, Electrical
Engineering and Automatic Control Universitat Rovira i Virgili, Tarragona,
Spain. Экспериментальное детектирование "bubbling" в однофазном инверторе.





\( O_{M^m} \), область \(\Pi_1^{(1)} \subset \Pi_1 \)

\( O_{M^{k_1}R^{k_2}M^{k_3}L^{k4}} \), где \( k_1 + k_2 + k_3 + k_4 = m, \) область \(\Pi_1^{(4)} \subset \Pi_1 \)

Более сложный тип периодических движений, область \(\Pi_1^{(*)} \subset \Pi_1 \)
"Border collisions" в области \( \Pi_1 \)

Исследование явления "bubbling"

Лаборатория проф. Abdelali El Aroudi, Department of Electronics, Electrical
Engineering and Automatic Control Universitat Rovira i Virgili, Tarragona,
Spain. Экспериментальное детектирование "bubbling" в однофазном инверторе.




Лаборатория проф. Abdelali El Aroudi, Department of Electronics, Electrical Engineering and Automatic Control Universitat Rovira i Virgili, Tarragona, Spain. Экспериментальное детектирование "bubbling" в однофазном инверторе.


Однофазный инвертор
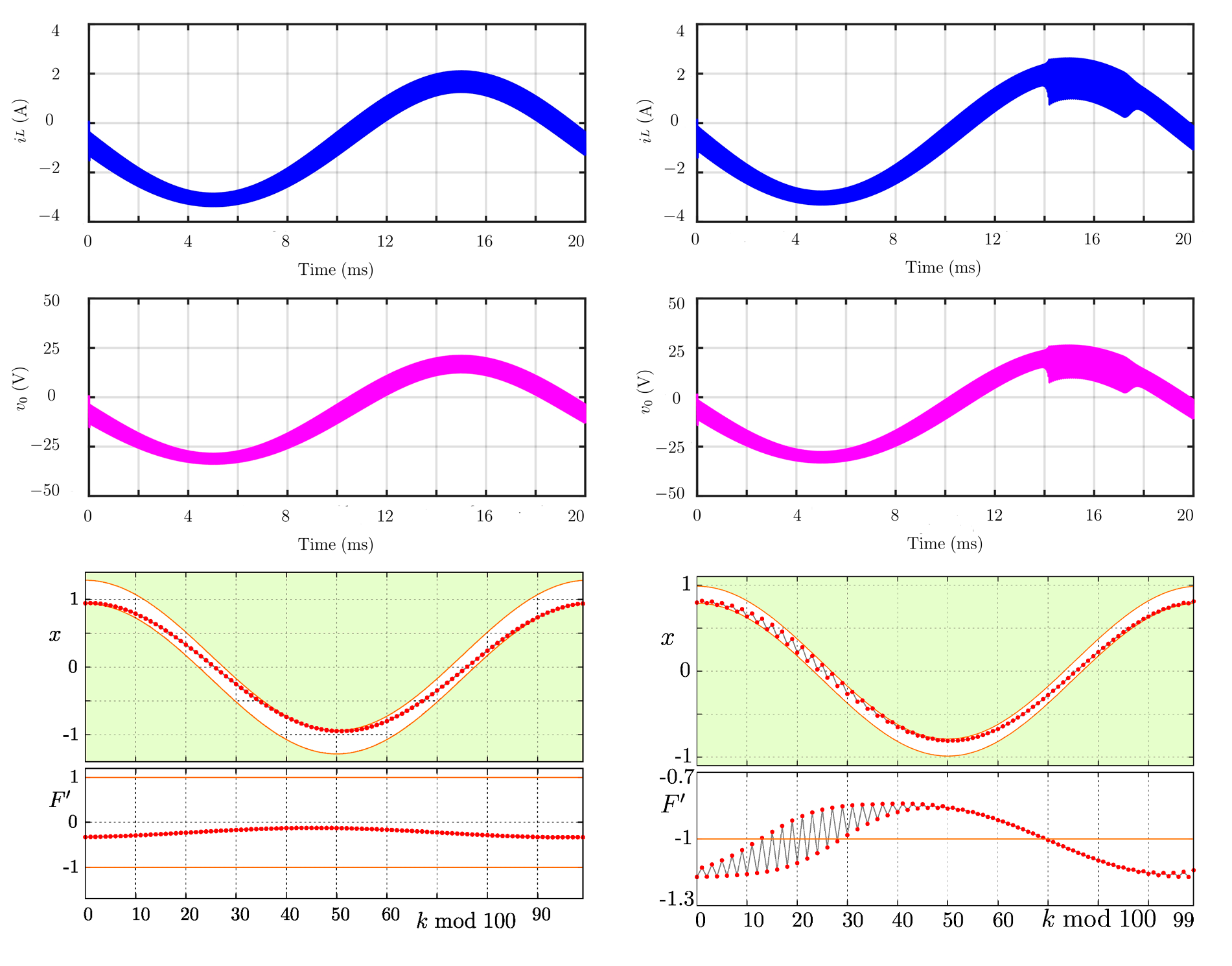
"Bubbling" индуцируется border, шумом после pitchfork и flip
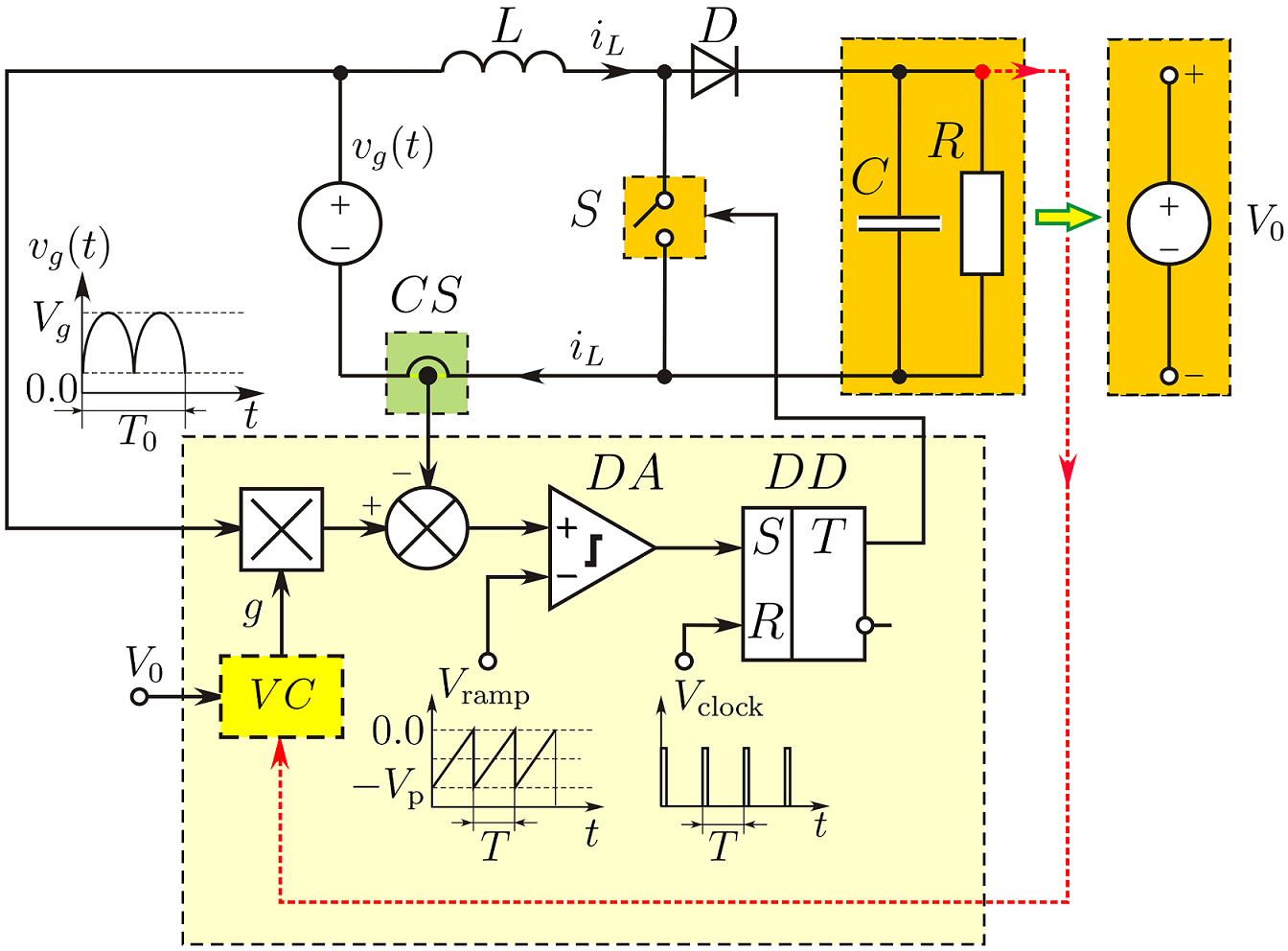
Корректор коэффициента мощности