Разрывные отображения

Совместные исследования со Штутгартским университетом (Германия) и Белгородским государственным технологическим университетом им. В.Г. Шухова (Россия).

В большинстве вибрационных машин и устройств, применяемых на практике (добыча и переработка полезных ископаемых, химическая промышленность, металлургия, строительство, приборостроение и т.д.), колебания возбуждаются механическими дебалансными вибровозбудителями. Такие вибровозбудители представляют собой неуравновешенные роторы, приводимые во вращение электродвигателями постоянного или переменного тока.

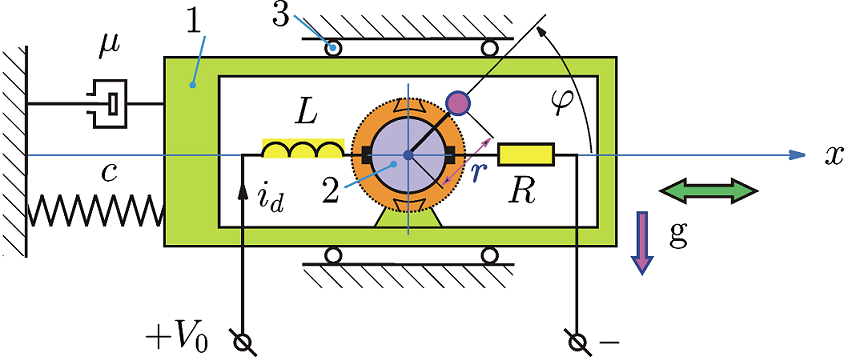
Вибрационная машина с дебалансными вибровозбудителем

На платформе 1 массой $m_{2}$ , связанной с неподвижным основанием линейным упругим элементом жесткости $c$ (пружиной) и демпфирующим элементом с коэффициентом вязкого трения $μ$ , установлен неуравновешенный ротор. Ротор приводится во вращение электродвигателем постоянного тока. Масса дебаланса $m_{1}$ сконцентрирована в точке, отстоящей от оси якоря электродвигателя 2 на расстояние $r$ . Горизонтальное движение платформы обеспечивается направляющими 3, например, на подшипниках качения. Уравнения движения этой системы имеют вид (Блехман И.И. Вибрационная механика. - М.: Физматлит, 1994.):

$\begin{matrix} (m_{1} + m_{2}) \frac{d^{2} x}{d t^{2}} + μ \frac{d x}{d t} + c x = m_{1} r [\frac{d^{2} φ}{d t^{2}} \sin φ + {(\frac{d φ}{d t})}^{2} \cos φ], \\ J \frac{d^{2} φ}{d t^{2}} - m_{1} r (\frac{d^{2} x}{d t^{2}} \sin φ - g \cos φ) = M (i_{d}), L \frac{d i_{d}}{d t} + R i_{d} + C_{ω} \frac{d φ}{d t} = V_{0}, \\ M (i_{d}) = C_{E} \cdot i_{d}, J = J_{d} + J_{r}, J_{r} = m_{1} r^{2}, \end{matrix}$ здесь $φ$ - угол поворота ротора, отсчитываемый от горизонтального направления; $x$ - перемещение платформы; $i_{d}$ - ток якоря двигателя; $m_{1}, J_{r}, r$ - соответственно масса, момент инерции ротора, эксцентриситет; $g$ - ускорение свободного падения; $m_{1} + m_{2}$ - масса системы; $J_{d}$ - момент инерции вала двигателя; $M (i_{d})$ - момент, передаваемый на ротор от электродвигателя; $L, R, C_{ω}, C_{E}$ - параметры двигателя; $V_{0}$ - напряжение питания.

Управление колебаниями вибрационной машины

Экспериментальная установка вибрационной машины с релейным управлением. Здесь 1,2 - вибрационная машина и система управления; 3, 4 - осциллограф и источник питания

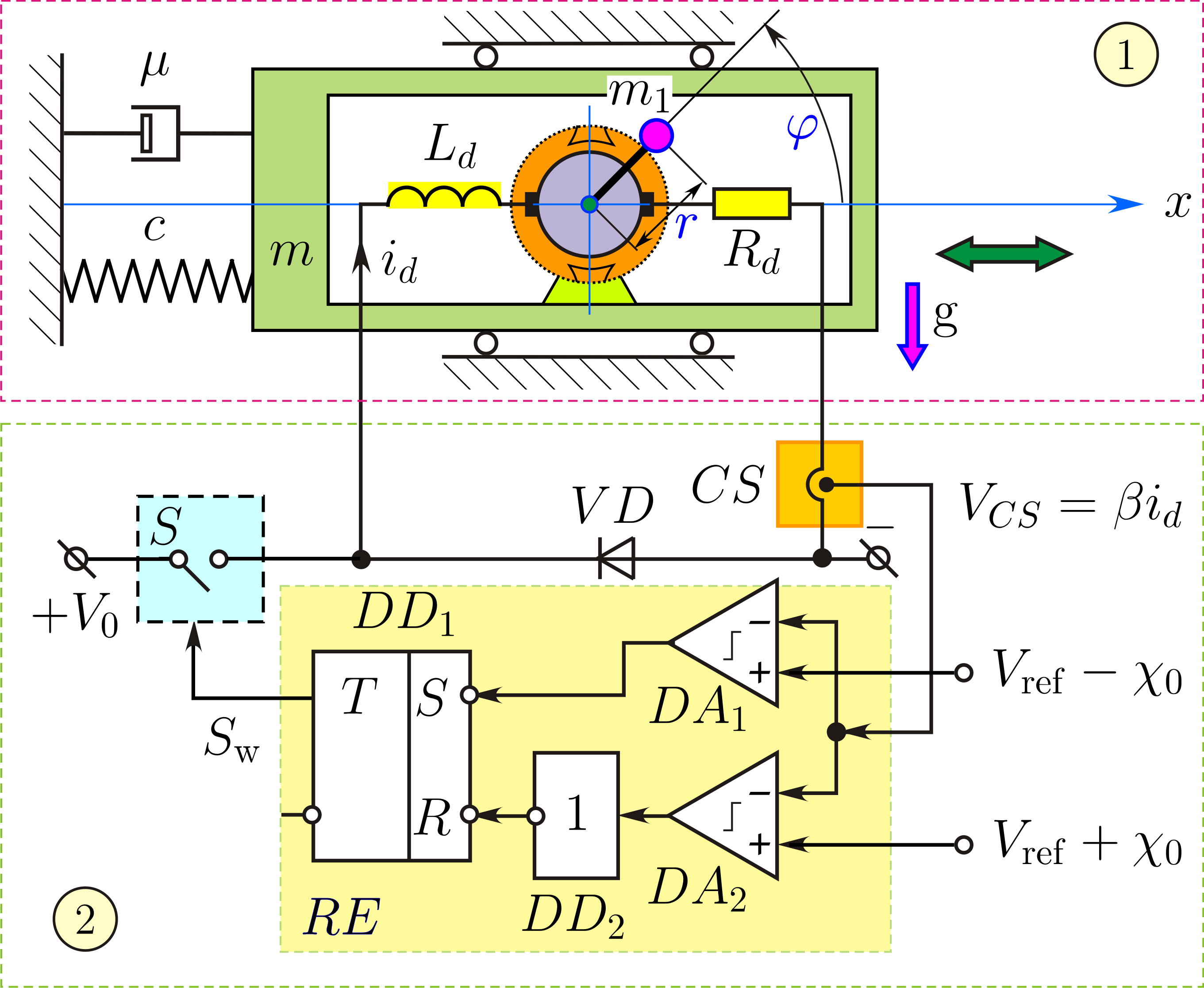
Функциональная схема системы

Математическая модель вибрационной машины с релейным автоматическим управлением

$\begin{matrix} (m_{1} + m_{2}) \frac{d^{2} x}{d t^{2}} + μ \frac{d x}{d t} + c x = m_{1} r [\frac{d^{2} φ}{d t^{2}} \sin φ + {(\frac{d φ}{d t})}^{2} \cos φ], \\ J \frac{d^{2} φ}{d t^{2}} - m_{1} r (\frac{d^{2} x}{d t^{2}} \sin φ - g \cos φ) = M (i_{d}), L_{d} \frac{d i_{d}}{d t} + R i_{d} + C_{ω} \frac{d φ}{d t} = V_{0} K_{F} (ξ, η), \\ M (i_{d}) = C_{E} \cdot i_{d}, J = J_{d} + m_{1} r^{2}, ξ = V_{ref} - β i_{d}, L_{d} = L_{d}^{*} + L_{F}, R_{d} = R_{d}^{*} + R_{F}, \end{matrix}$ Выходной сигнал $S_{w}$ релейного элемента описывается коммутационной функцией $K_{F} (ξ, η)$ : $K_{F} (ξ, η) = {\begin{cases} 1, & if (ξ > + χ_{0}) or ((- χ_{0} \leq ξ \leq χ_{0}) and (η = 1)), \\ 0, & if (ξ < - χ_{0}) or ((- χ_{0} \leq ξ \leq χ_{0}) and (η = 0)) \end{cases}$

Здесь $ξ, χ_{0}$ - входной сигнал и гистерезис релейного элемента; $η$ - предыдущее состояние релейного элемента; $V_{r e f}$ - сигнал задания момента $M (i_{d})$ двигателя; $β$ - чувствительность датчика тока якоря; $C_{E}, C_{ω}$ - постоянные электрической машины; $L_{d}^{*}, R_{d}^{*}$ - индуктивность и сопротивление обмотки якоря; $L_{F}, R_{F}$ индуктивность и сопротивление сглаживающего фильтра.
Если $K_{F} = 1$ , то силовой ключ $S$ замкнут (силовой транзистор открыт) и если $K_{F} = 0$ , то ключ $S$ разомкнут (транзистор закрыт).

Параметры двигателя MAXON RE 25:
$L_{d}^{*} = 0.238 \cdot 10^{- 3}$ Гн, $R_{d} = 2.18$ Ом, $C_{ω} = 0.02353$ В·c/рад, $C_{E} = 23.5 \cdot 10^{- 3}$ Н · м/А, $J_{d} = 1.08 \cdot 10^{- 6}$ кг · м².
Параметры системы управления и механической части:
$V_{r e f} = 0.5$ В, $β = 1$ В/А, $χ_{0} = 0.02$ В, $r = 0.01$ м, $m_{1} = 0.02$ кг, $m = m_{1} + m_{2} = 0.2$ кг, $c = 250$ Н/м, $μ = 102.5$ кг/с, $R = R_{d} + R_{F} = 2.68$ Ом, $L = L_{d} + L_{F} = 1.238 \cdot 10^{- 3}$ Гн, $V_{0} > 11.8$ В.

Результаты численных экспериментов. Явление синхронизации

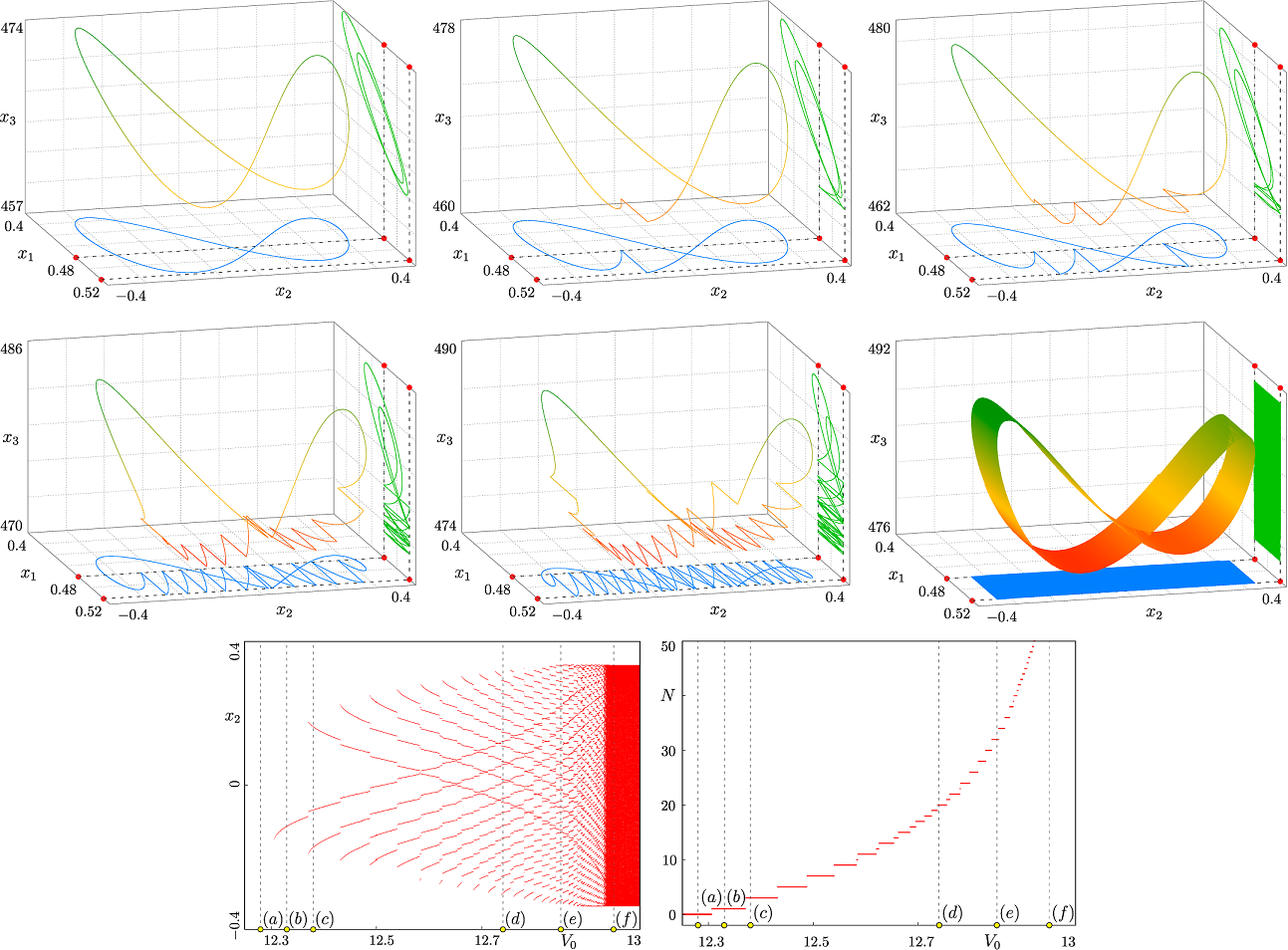
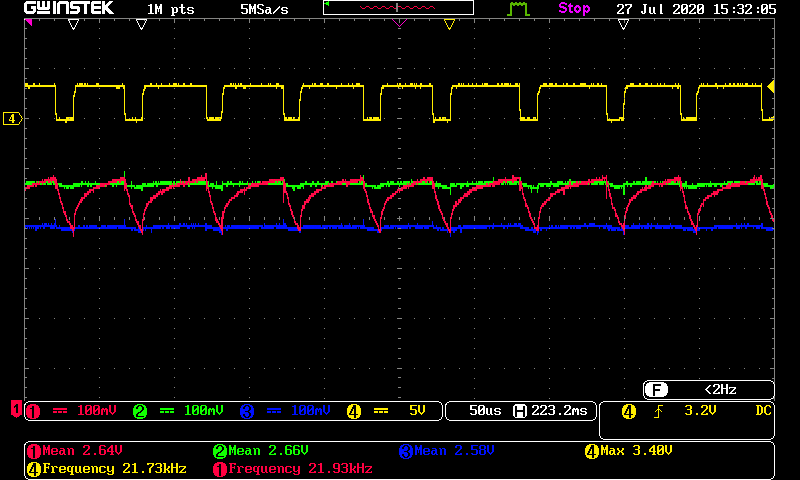
Результаты экспериментальных исследований динамических режимов на установке

Сведение многомерной динамической системы к маломерной с двумя масштабами времени

Уравнение движения:

\begin{matrix} L \frac{d i_{d}}{d t} + R i_{d} + C_{ω} ω (t) = V_{0} K_{F} (ξ, η), ω (t) = \frac{d φ}{d t} = ω_{0} + ω_{m} \cos (Ω t), \\ ω_{0} = \frac{V_{0} - V_{ref} R_{d} / β}{C_{ω}}, ω_{m} = \frac{\sqrt{1 + T_{d}^{2} Ω^{2}} R_{d}}{C_{ω}^{2}} Δ M, T_{d} = \frac{L_{d}}{R_{d}}, \\ Δ M = 0.5 C_{E} (V_{ref} + χ_{0} - β i_{d}^{*}) / β, i_{d}^{*} = min_{0 ⩽ t ⩽ T} i_{d} (t) . \end{matrix}

Уравнение движения в безразмерной форме

\begin{matrix} \dot{x} = λ (x - K_{F} (x, η) + γ_{0} + γ_{m} \cos (τ)), \\ K_{F} (x, η) = {\begin{cases} 1, if q - x > + χ or (| q - x | < χ and η = 1); \\ 0, if q - x < - χ or (| q - x | < χ and η = 0) . \end{cases} \end{matrix}

γ_{0} = \frac{C_{ω} ω_{0}}{V_{0}}, γ_{m} = \frac{C_{ω} ω_{m}}{V_{0}}, λ = - \frac{R_{d}}{L_{d} Ω}, q = \frac{V_{ref} R_{d}}{β V_{0}}, χ = \frac{R_{d} χ_{0}}{β V_{0}} .

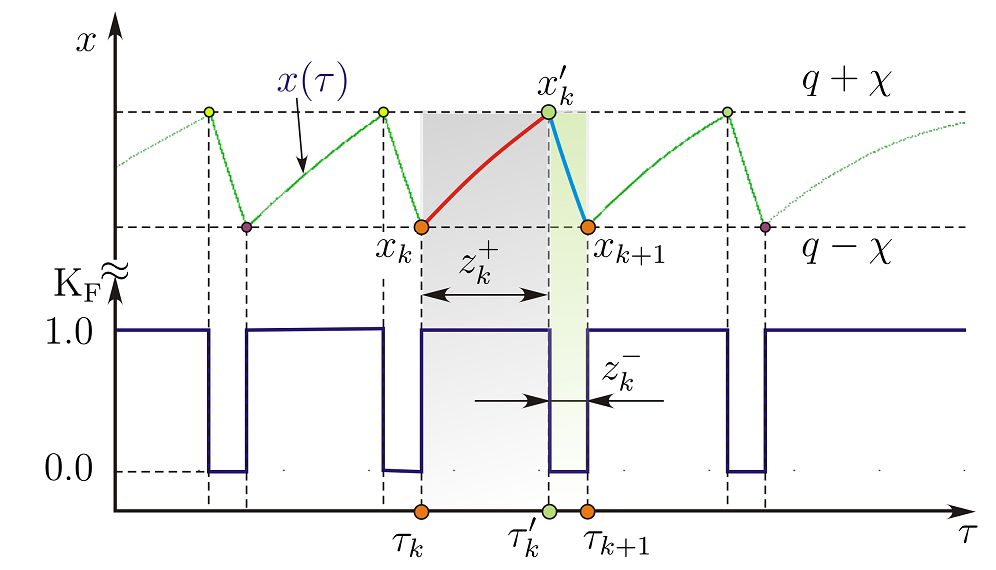
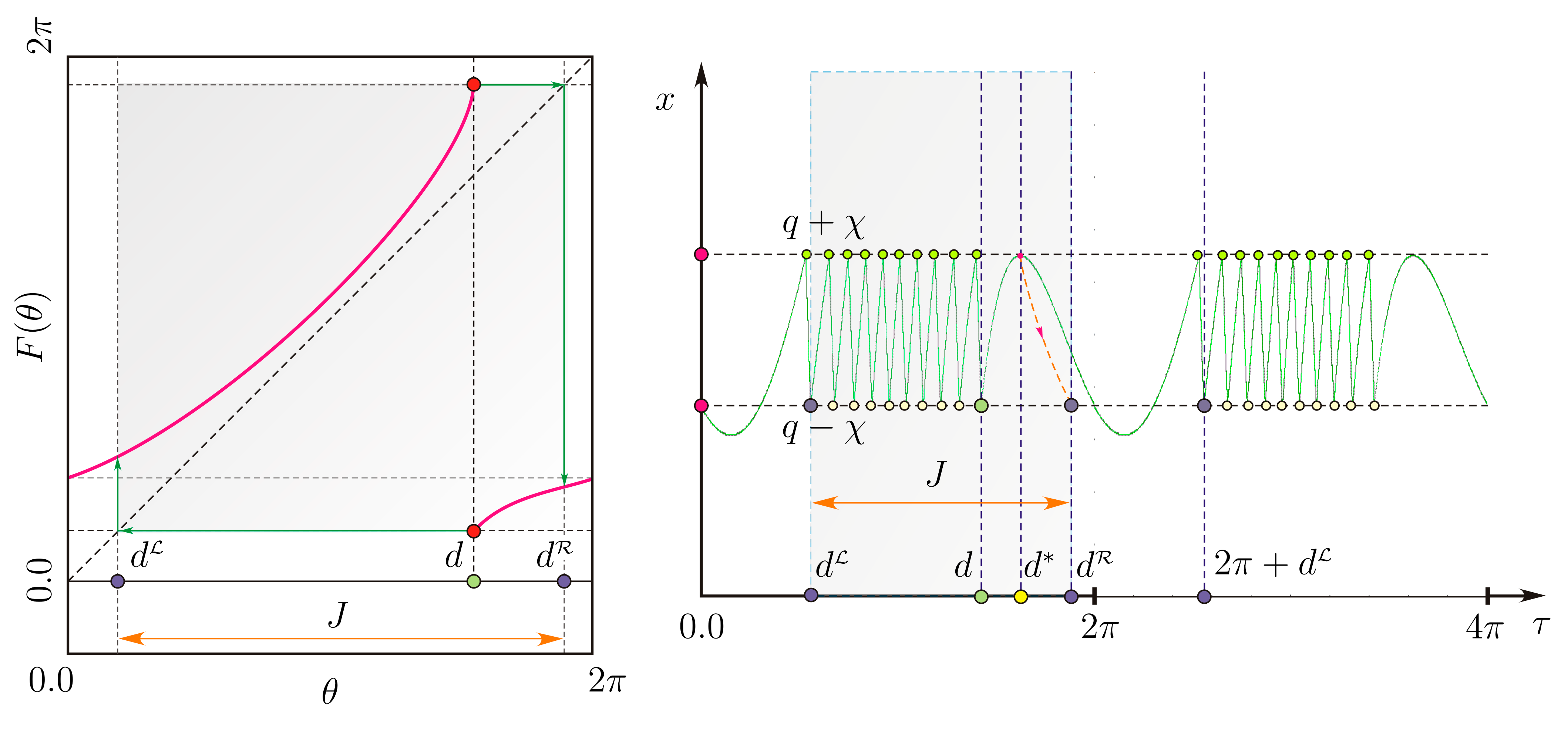
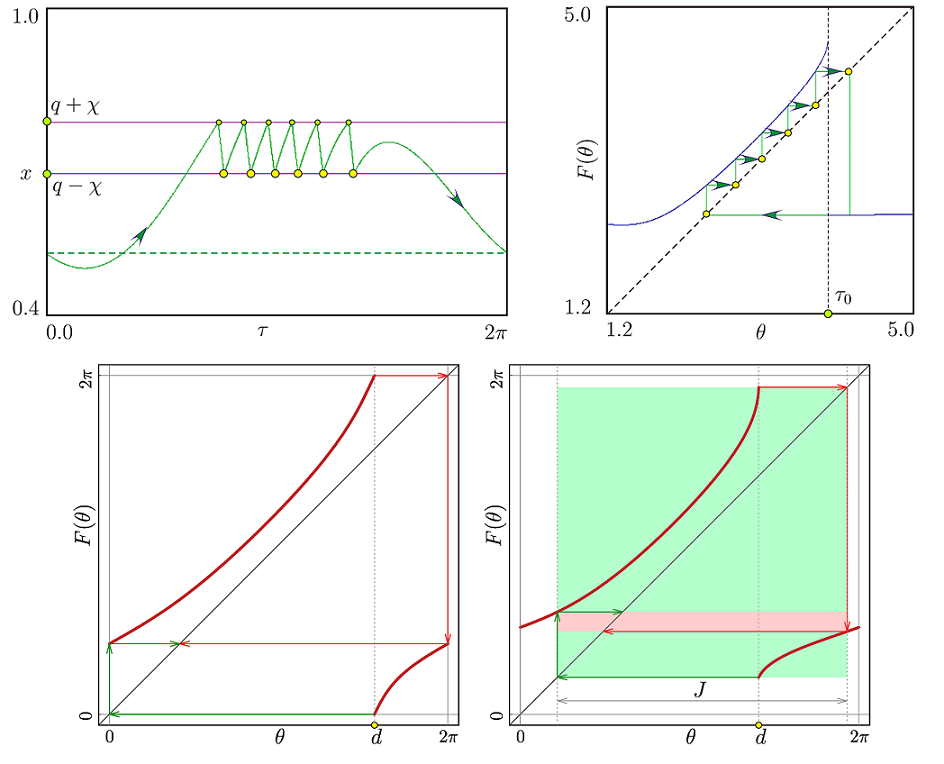
Построение разрывного отображения окружности

θ_{k + 1} = F (θ_{k}) = f^{-} \circ f^{+} (θ_{k}) = θ_{k} + z_{k}^{+} + z_{k}^{-} mod 2 π,

где

θ_{k}

- фаза в k-й момент переключения релейного элемента,

z_{k}^{+}

z_{k}^{-}

- коэффициенты заполнения импульсов.

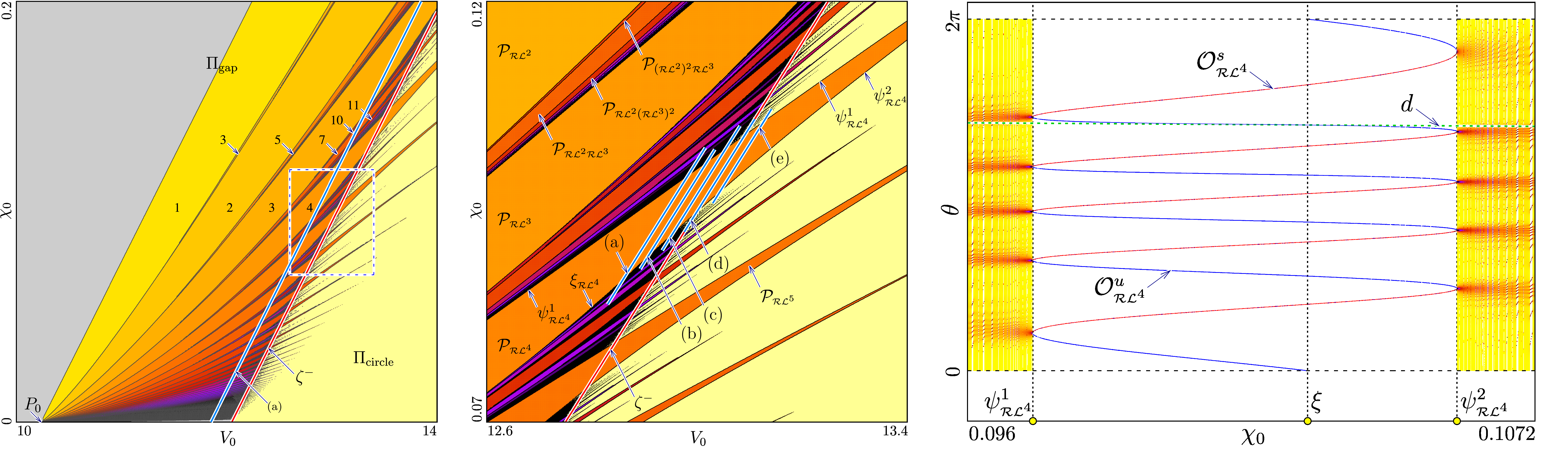
Бифуркационная структура

Основные публикации по результатам исследований

Zh. T. Zhusubaliyev, V. Avrutin½ V. G. Rubanov, D. A. Bushuev, D. V. Titov, and O. O. Yanochkina, Persistence Border Collisions in a Vibrating System Excited by an Unbalanced Motor With a Relay Control. 8th Polyakhov's Reading: Proceedings of the International Scientific Conference on Mechanics// American Institute of Physics (AIP) Conference Proceedings,1959, 2018, (080022-1 - 080022-8).
Zh. T. Zhusubaliyev, V. Avrutin, V. G. Rubanov c, D. A. Bushuev, Complex dynamics of a vibration machine caused by a relay feedback control// Physica D: Nonlinear Phenomena, 420, 132870 (15 pages),2021 (impact factor 2.3, квартиль Q1).
Zh. T. Zhusubaliyev, V. Avrutin, V. G. Rubanov, D. A. Bushuev, D. V. Titov, and O. O. Yanochkina, Persistence border collisions in a vibration system with a relay control// 2018 International Symposium on Nonlinear Theory and Its Applications, NOLTA2018, Tarragona, Spain, September 2-6, 2018, 332 - 334.
Zh. T. Zhusubaliyev, V. Avrutin, Border-collisions in a periodically forced self-oscillatory piecewise smooth system with a high number of switching manifolds//15th International Conference Dynamical Systems - Theory and Applications, DSTA, December 2-5, 2019. Lodz, Poland.