Автоматическое управление нейромышечной блокадой

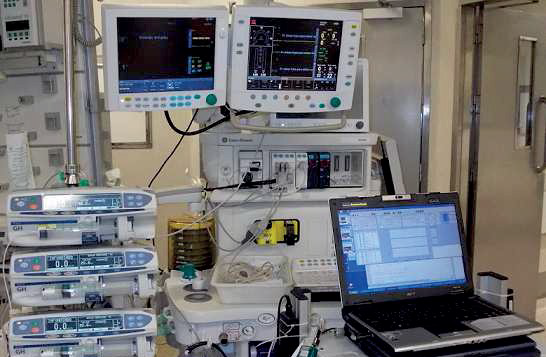
Оборудование на платформе Galeno (из PhD диссертации Margarida M. Silva [1])

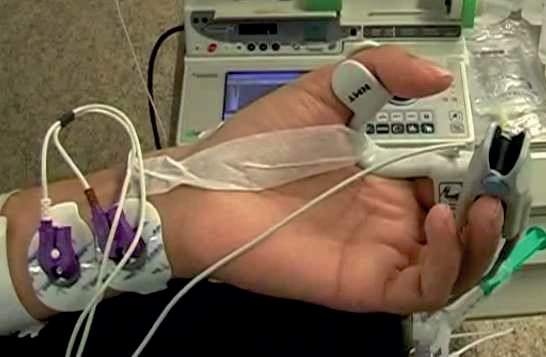
Измерение уровня нейромышечной блокады (Hospital de Santo Antonio, Porto, из PhD диссертации Margarida M. Silva [1])

Математическая модель

Структурная схема ПИД регулятора системы автоматического управления НМБ

Стандартные физиологически обоснованные модели, описывающие взаимосвязь между введенной дозой анестетика u(t) и его эффектом, можно разделить на четыре каскадных блока, показанных на рисунке.

• Первый блок связывает дозу анестетика u(t) с его концентрацией \(c_p\) (t) в плазме крови. Это составляет модель фармакокинетики PK (PK - pharmacokinetics).
• Второй блок связывает концентрацию препарата в плазме крови \(c_p\) (t) с концентрацией препарата на месте его действия c(t): в случае миорелаксантов - нервномышечном соединении, а в случае снотворных и анальгетиков - в головном мозге.
• Третий блок описывает взаимосвязь между концентрацией c(t) и наблюдаемым эффектом \(c_e\) (t). Эти два блока представляют динамическую часть и описывают фармакодинамикy (PD - pharmacodynamics), т.е. распределение лекарств в организме, которое зависит от нескольких транспортных и метаболических процессов.
• Четвертый блок представляет нелинейность PD и связывает концентрацию эффекта \(c_e\) (t) с эффектом препарата в количественном выражении по измеренному уровню y(t) нейромышечной блокады NMB. Параметры этой функции необходимо оценить на основе клинических данных.

Управляющий сигнал u(t) формирует ПИД регулятор (PID): \( u(t)=K\left(\varepsilon(t)+T_i\int\varepsilon(s) ds+T_d\dfrac{d\varepsilon}{dt}\right) \), \(\varepsilon(t)=y_\mathrm{ref}-y(t)\).

При наличии надежных моделей фармакокинетики (PK) и фармакодинамики (PD) можно избежать недодозировки или передозировки, запрограммировав шприцевые насосы на целевые значения эффективности препарата. Существует несколько моделей, одна из них, называемая "минимально параметризованная" (minimally parameterized), имеет вид: $$\mathbf{\dot{x}}=\mathbf{f}(\mathbf{x}),\quad \mathbf{x}=(x_1,x_2,x_3,x_4)^T,\quad \mathbf{f}(\mathbf{x})=(f_1,f_2,f_3,f_4)^T,$$ \begin{gather*} f_1=-\alpha\,k_3\,x_1- \alpha^2\,k_1\,k_3\,K\,T_d\,\Phi'(x_3)(x_2-x_3) +\alpha\,k_3\,K (y_{\text{ref}}-\Phi(x_3))+\tfrac{\alpha k_3\,K}{T_i}x_4, \quad \Phi(x_3)=\tfrac{100\,C_{50}^\gamma}{C_{50}^\gamma+x_3^\gamma};\\[-0.8ex] f_2=\alpha\,k_2(x_1-x_2);\quad f_3=\alpha k_1(x_2-x_3);\quad f_4=y_{\text{ref}}-\Phi(x_3). \end{gather*}

Пример бифуркационного анализа

Бифуркационный анализ

Публикации результатов исследований:

1. Zh. T. Zhusubaliyev, A. Medvedev, M. Silva, Bifurcation Analysis for PID-controller Tuning Based on a Minimal Neuromuscular Blockade Model in Closed-loop Anesthesia// 52nd IEEE Conference on Decision and Control, Firenze, Italy,2013.
2. Zh.T. Zhusubaliyev, A. Medvedev, M. Silva, Nonlinear Dynamics in Closed-loop Anesthesia: Pharmacokinetic/Pharmacodynamic Model under PID-feedback//The 2014 American Control Conference (ACC 2014), Portland, Oregon, USA.
3. Zh. T. Zhusubaliyev, M. Silva, A. Medvedev, Automatic Recovery From Nonlinear Oscillations in PID-Controlled Anesthetic Drug Delivery// European Control Conference (ECC 2015), Linz, Austria, 2015.
4. Zh. T. Zhusubaliyev, A. Medvedev, M. Silva M, Bifurcation Analysis of PID Controlled Neuromuscular Blockade in Closed-loop Anesthesia//Journal of Process Control, 25, 152-163, 2015, (Impact Factor 3.666, квартиль Q1).
5. A. Medvedev, Zh. T. Zhusubaliyev, O. Rosen, M. M. Silva, Oscillations-free PID control of anesthetic drug delivery in neuromuscular blockade//Computer Methods and Programs in Biomedicine, 171 119-131, 2019, (Impact Factor 5.428, квартиль Q1).